Funkcje trygonometryczne to takie funkcje, które wyrażają związek między bokami i kątami w trójkącie prostokątnym - jeśli znamy boki trójkąta, to te funkcje pozwalają nam wyznaczyć jego kąty. Są one bardzo przydatne w zagadnieniach związanych z geometrią, choć na poziomie podstawowym nie ma niestety za dużo okazji, by tego doświadczyć.
Mamy takich funkcji sześć, ale w szkole uczycie się o trzech. Są to sinus, cosinus i tangens. Oznaczamy je jako , i . Należy pamiętać, że wartości funkcji wyznaczamy zawsze dla jakiegoś kąta. Tak więc zapis np. jest bez sensu - możemy zapisać, że , albo że . Oczywiście kąt nie musi nazywać się , równie dobrze może to być np. , czy .
Jak wyznaczyć wartości tych funkcji? Narysujmy sobie trójkąt prostokątny i nazwijmy jakoś kąty w tym trójkącie.
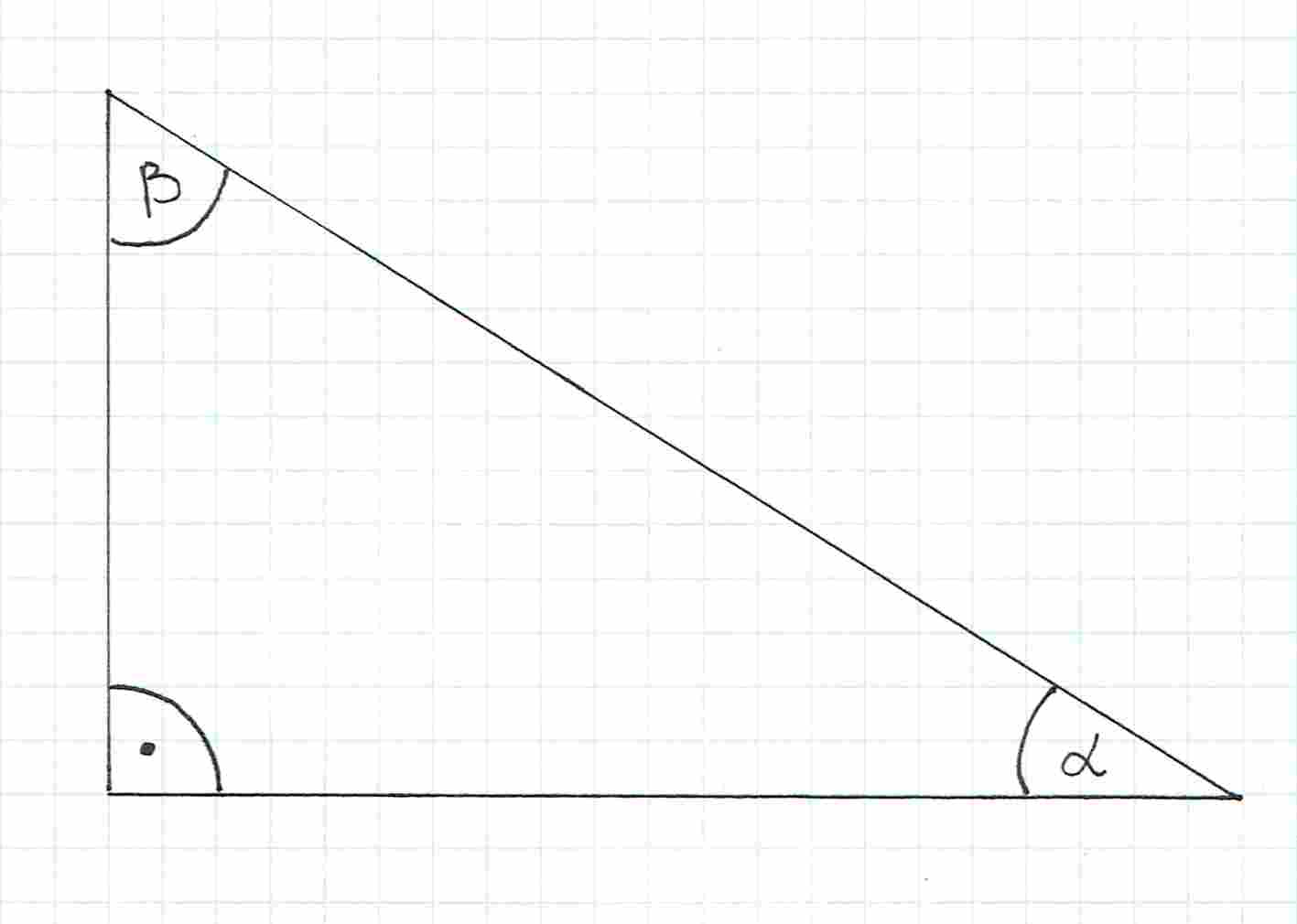
Powiedzmy, że chcemy wyznaczyć wartości funkcji dla kąta . Nazywamy teraz odpowiednio boki trójkąta. Bok, który jest naprzeciwko kąta , oznaczamy jako .
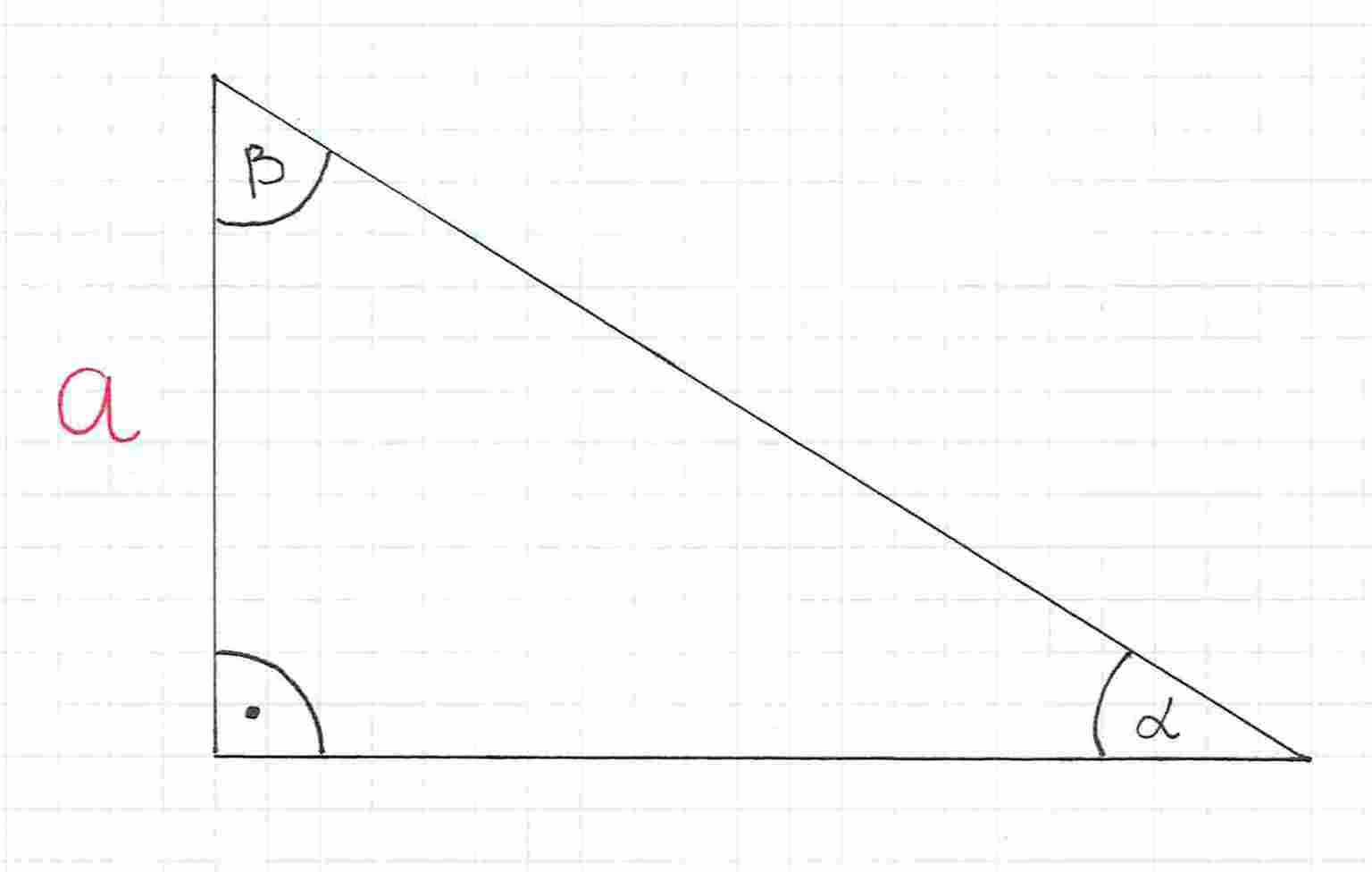
Drugą przyprostokątną oznaczamy jako .
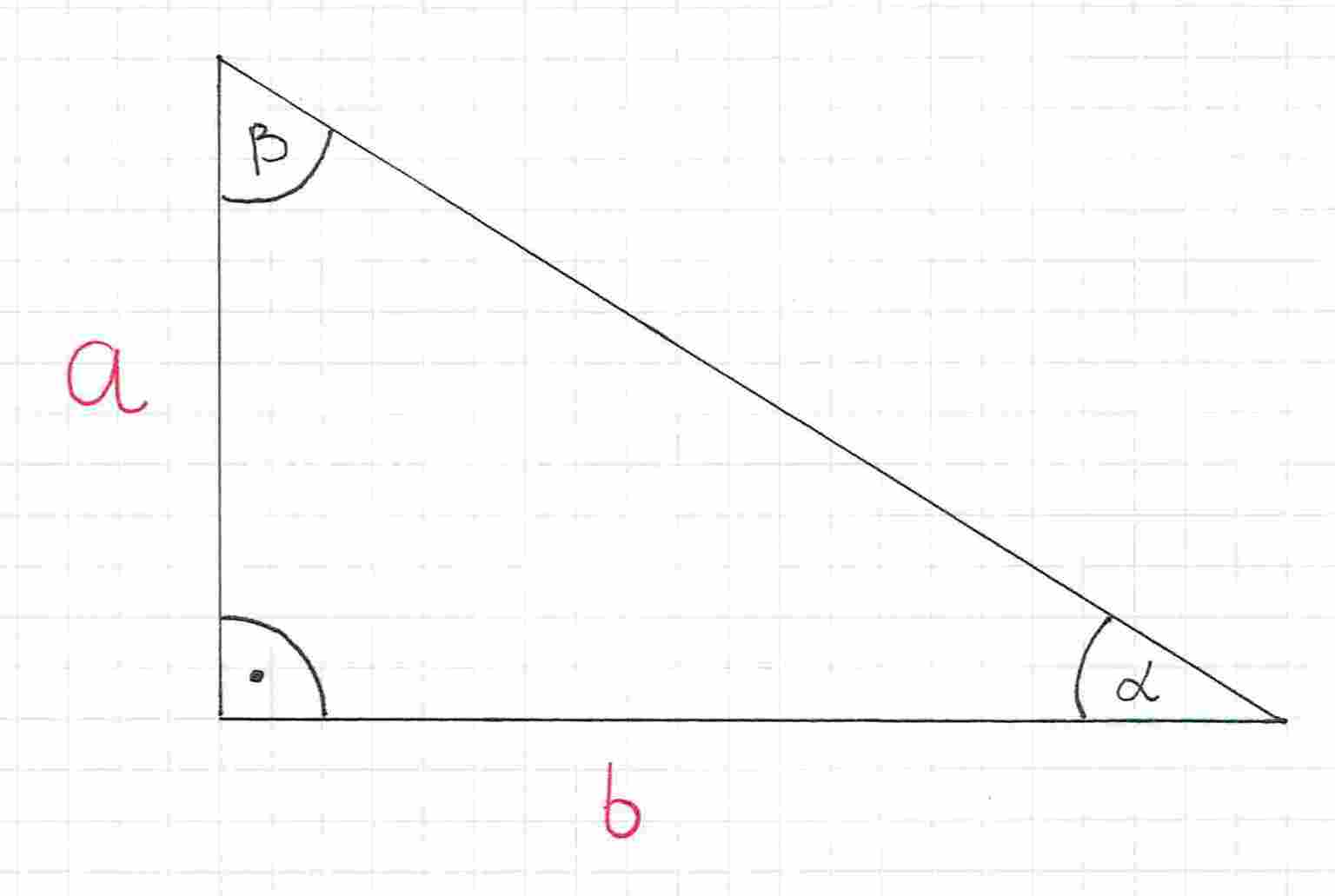
Natomiast przeciwprostokątną oznaczamy jako .
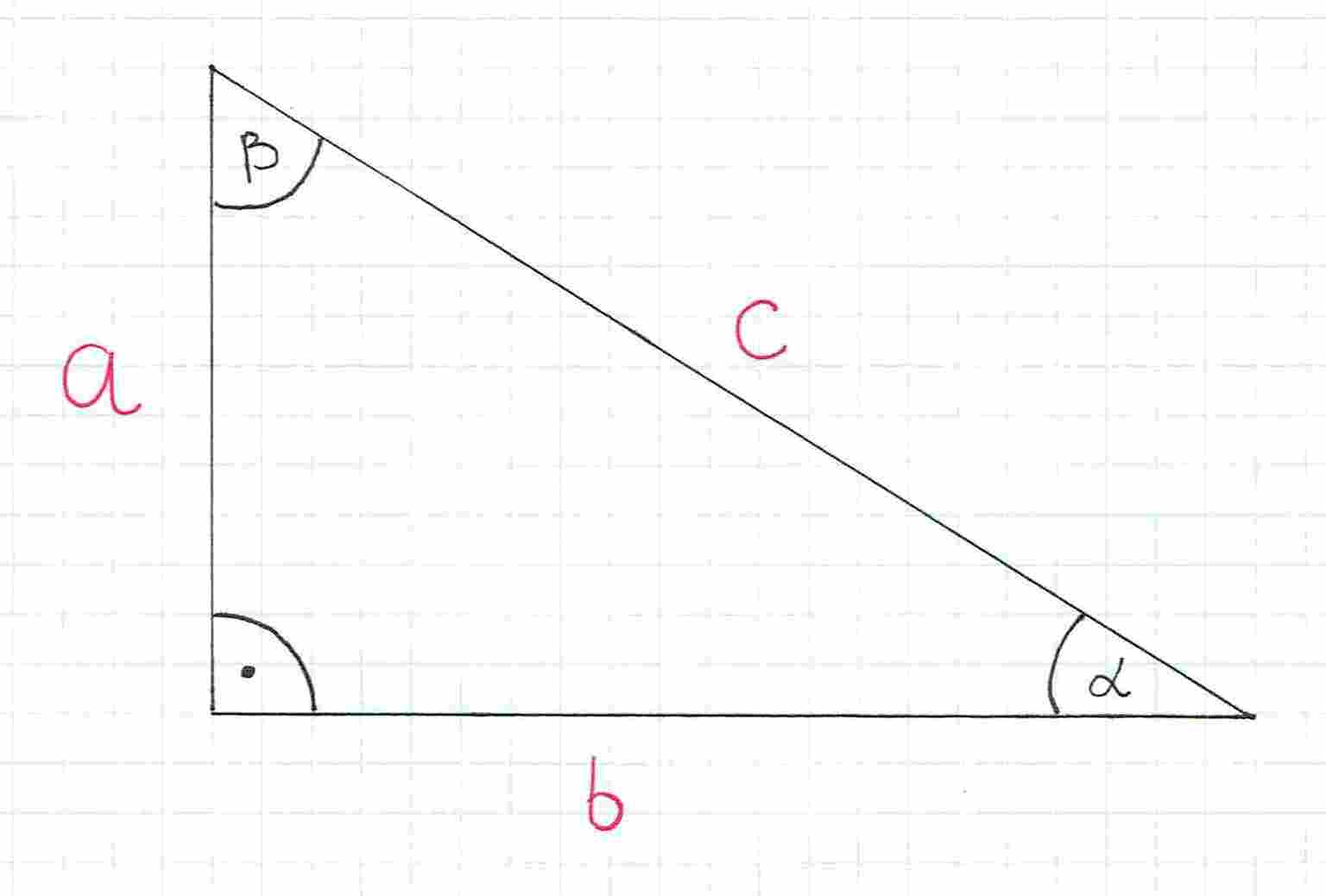
Dla tak oznaczonych boków wzory dla kąta wyglądają następująco:
Przećwiczmy sobie używanie tych wzorów. Niech dany będzie trójkąt prostokątny przedstawiony na rysunku. Wyznacz sinus kąta oraz tangens kąta .
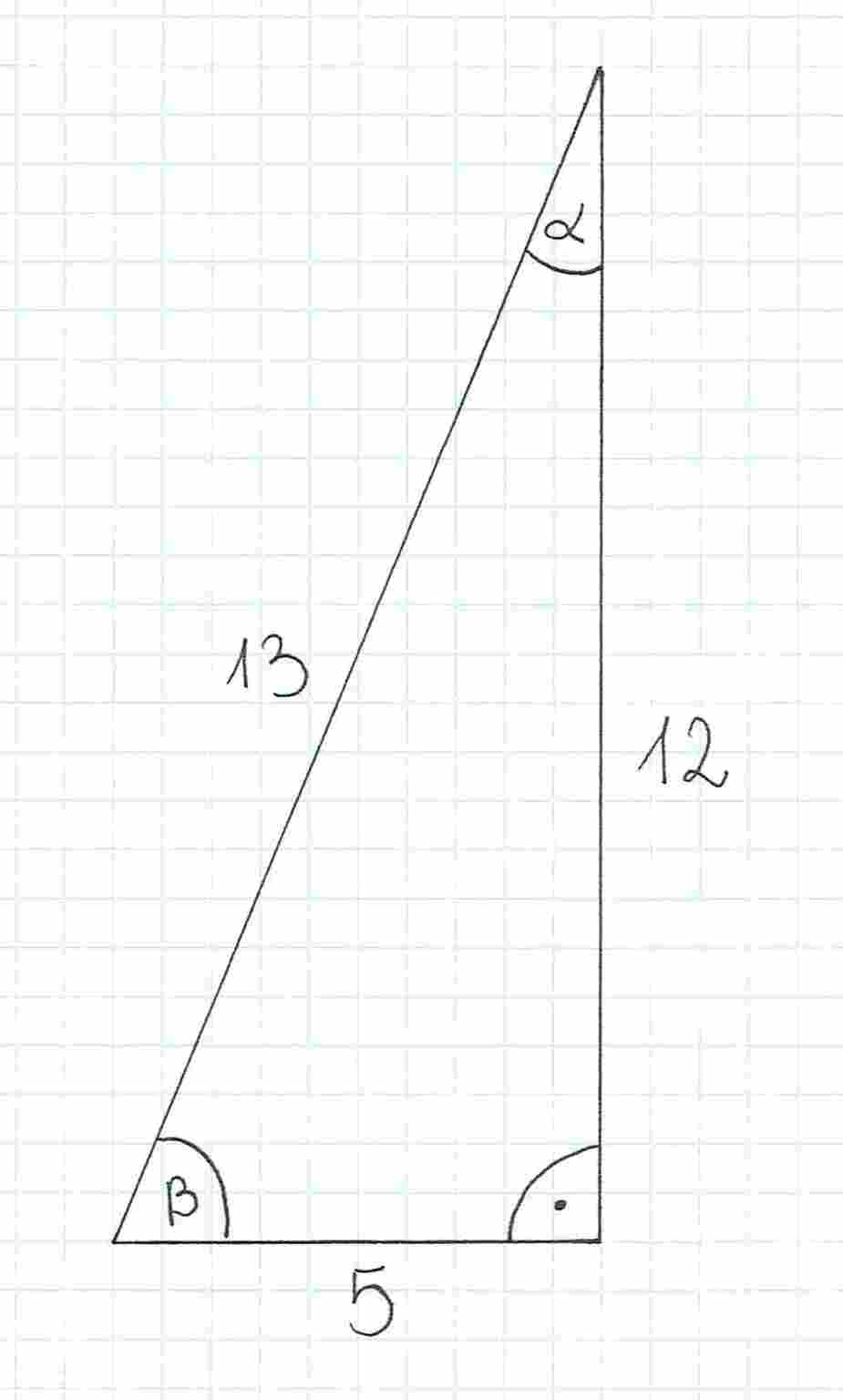
Wykonajmy najpierw pierwszą część polecenia, czyli wyznaczmy sinus kąta . Zaczynamy od tego, że nazywamy odpowiednio boki. Naprzeciwko kąta, który nas interesuje (czyli kąta ), znajduje się bok . Druga przyprostokątna to bok , a przeciwprostokątna to bok .
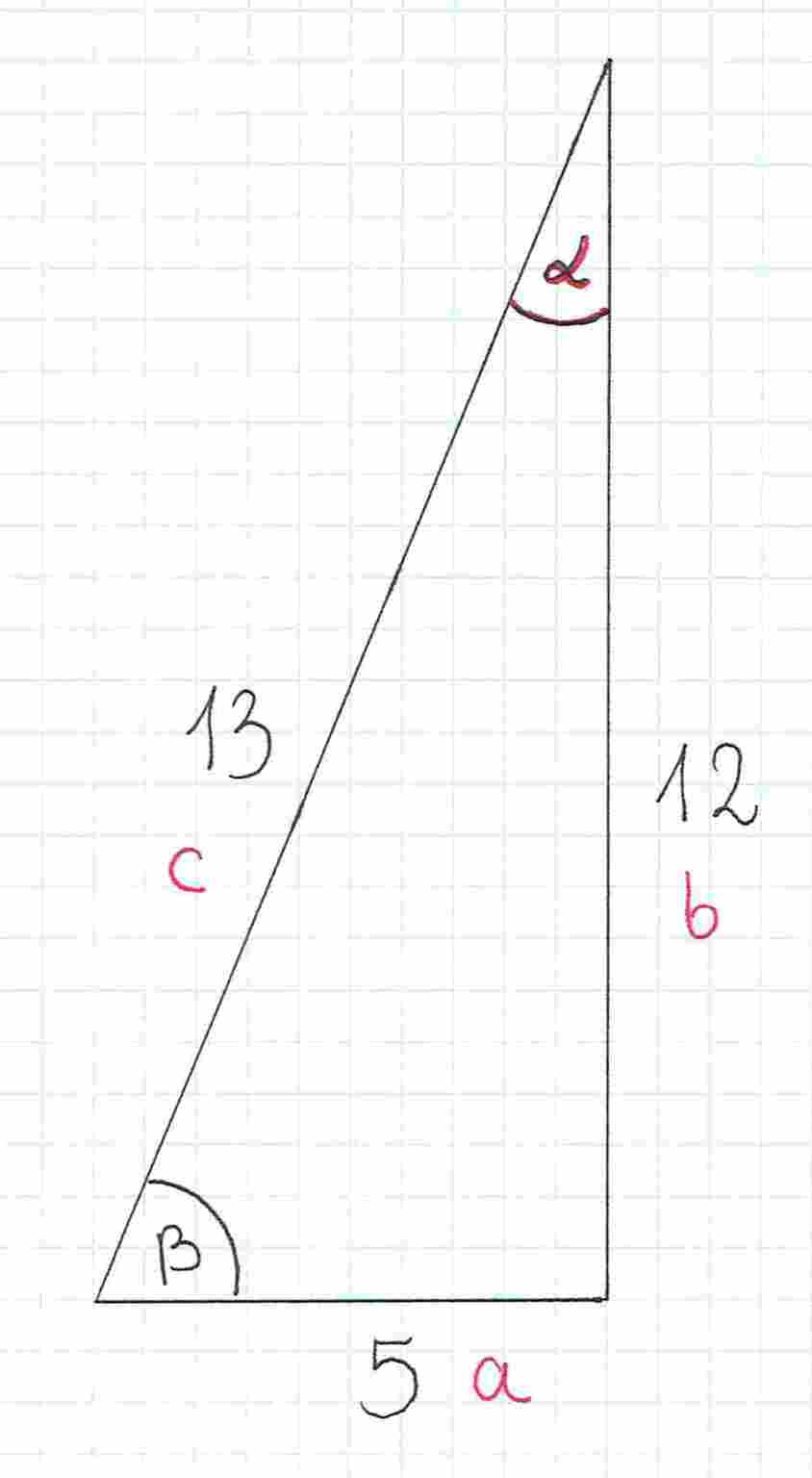
Chcemy wyznaczyć . Wybieramy odpowiedni wzór i podstawiamy do niego długości boków:
Następnie wykonamy drugą część zadania, czyli wyznaczymy tangens kąta . Zwróć uwagę, że teraz wyznaczamy wartość funkcji dla innego kąta, a to oznacza, że musimy od nowa ponazywać sobie boki. Naprzeciwko kąta, który nas interesuje (czyli tym razem kąta ), znajduje się bok . Druga przyprostokątna to bok . Przeciwprostokątna, czyli bok , zostaje bez zmian. Stare oznaczenia możemy po prostu skreślić.
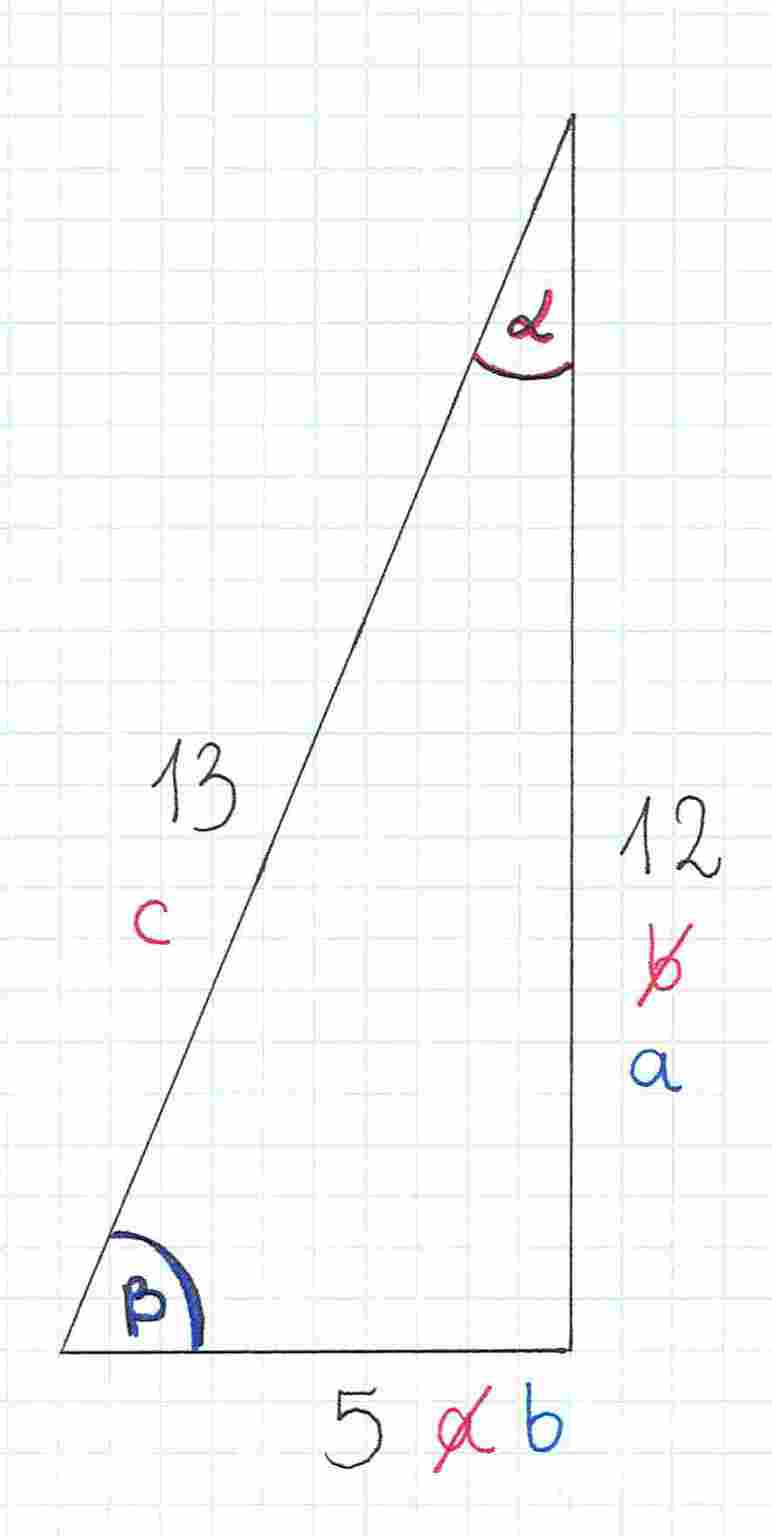
Teraz wybieramy odpowiedni wzór. Chcemy wyznaczyć , więc wybieramy wzór na tangens. Następnie podstawiamy do niego liczby.
Jak widzisz, stosowanie tych wzorów nie jest zbyt skomplikowane, należy tylko pamiętać o tym, by odpowiednio oznaczyć boki.
Teraz zróbmy takie zadanie:
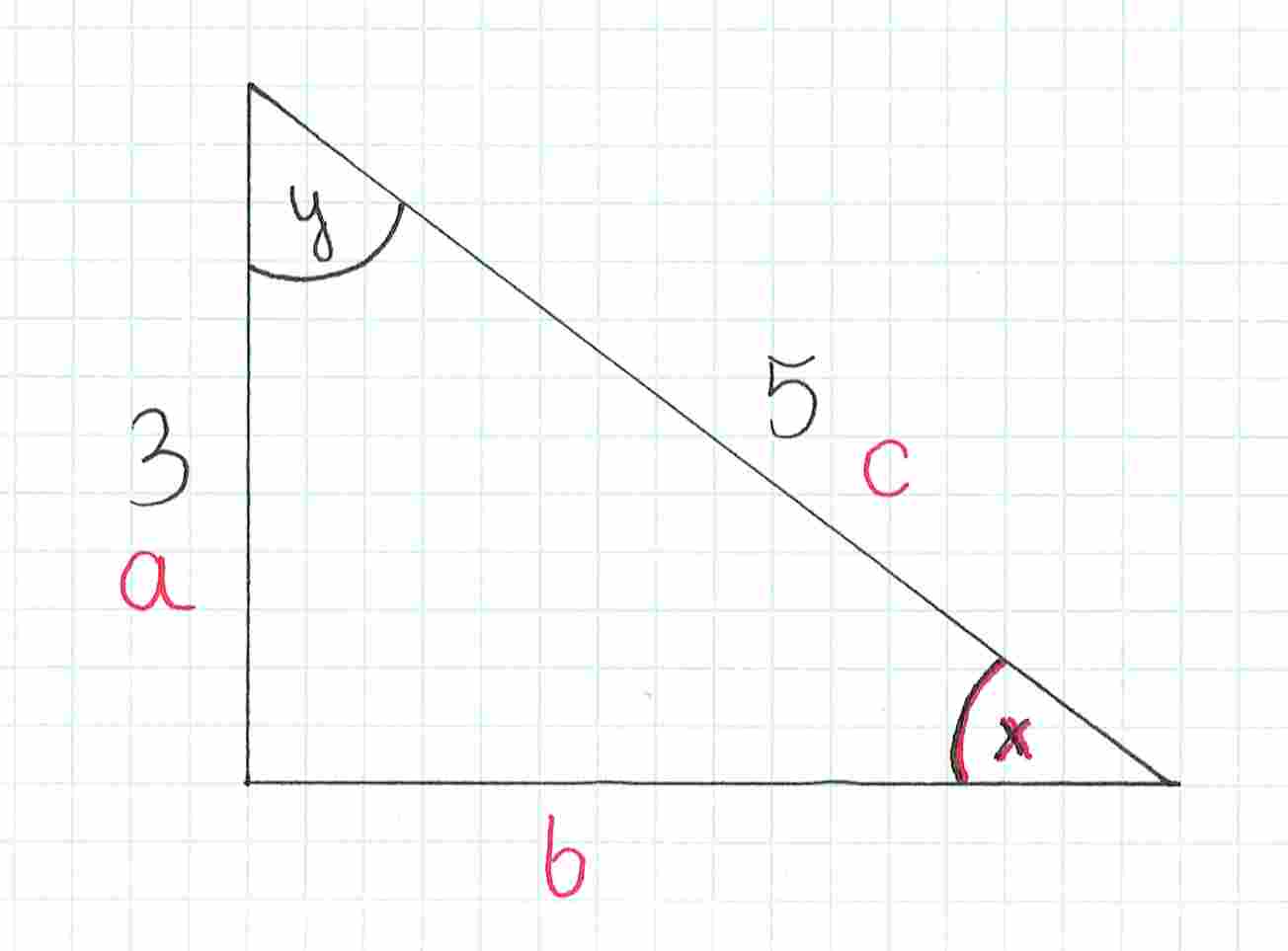
Dany jest trójkąt przedstawiony na rysunku. Wyznacz cosinus kąta .
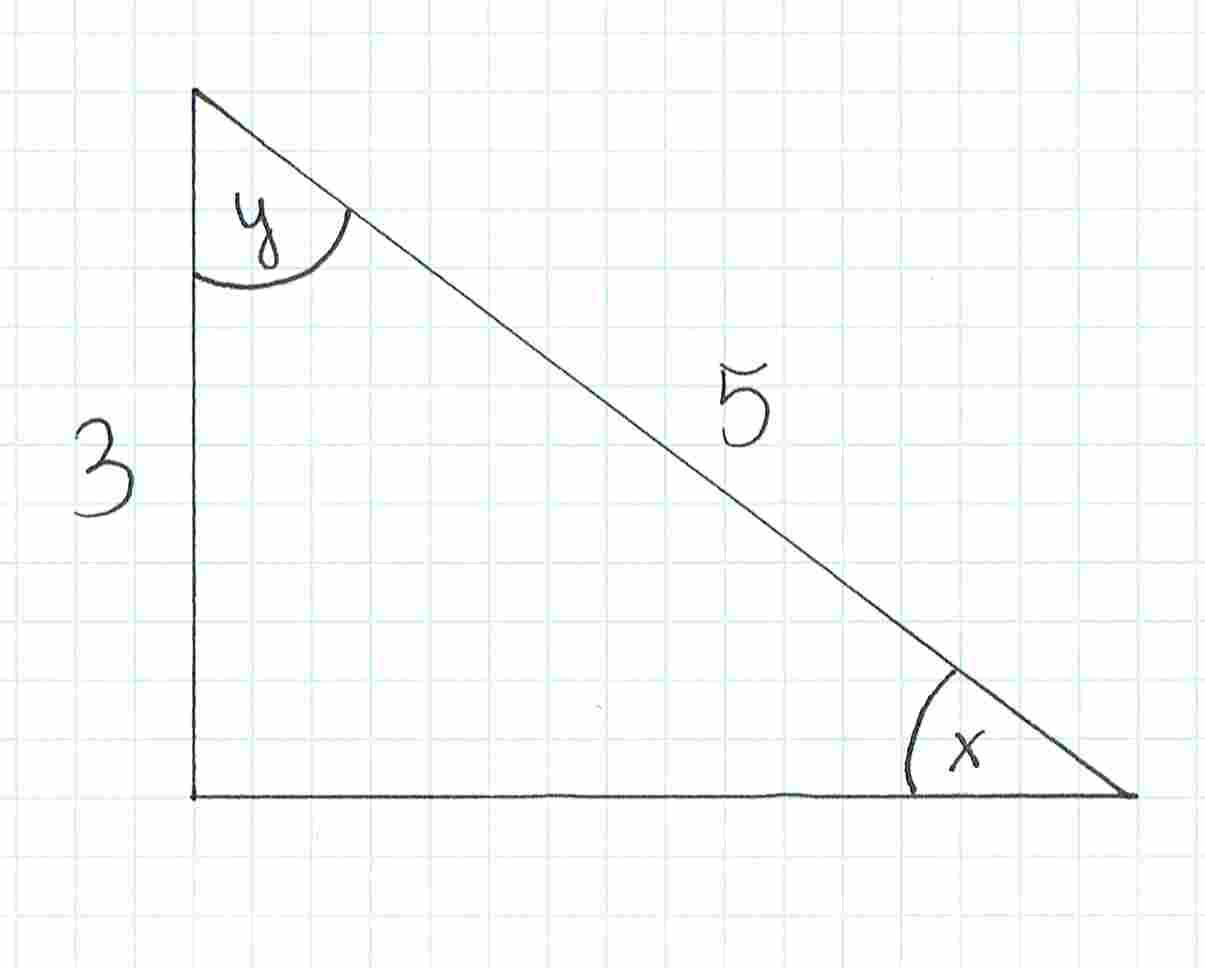
Zaczynamy od odpowiedniego oznaczenia boków. Chcemy wyznaczyć wartość cosinusa dla kąta , a więc naprzeciwko tego kąta zaznaczamy bok . Druga przyprostokątna to bok , natomiast przeciwprostokątna to bok .
Teraz szukamy wzoru na cosinusa.
Jak widzisz, nie możemy podstawić liczb do wzoru, bo nie mamy długości . Możemy ją jednak obliczyć, korzystając z twierdzenia Pitagorasa:
Teraz możemy już wyznaczyć cosinus:
Jeśli chodzi o wyznaczanie wartości funkcji trygonometrycznych w trójkącie, to tyle na dziś. Zapraszam Cię do następnych części 🙂 A jeśli chcesz wiedzieć, po co w zasadzie jest ten cosinus, to zerknij tutaj.