Wyznaczanie wzoru funkcji to klasyczne zadanie maturalne. Jest ono znacznie prostsze, niż się z pozoru wydaje 😉 Przejdźmy od razu do przykładów. Zaczniemy od najprostszego wariantu i stopniowo będziemy zwiększać trudność.
Dana jest funkcja . Punkt należy do wykresu tej funkcji. Wyznacz jej wzór.
Na początek dwie uwagi.
Po pierwsze: polecenie brzmi "wyznacz wzór funkcji", więc zastanówmy się, co to w ogóle znaczy - w końcu w poleceniu już jest wzór: . Aby wzór był wzorem, muszą w nim występować oraz (lub ) - i to są jedyne niewiadome, które powinny się w nim znaleźć. Czyli nasz wzór jeszcze nie jest gotowy - musimy poznać, jaką liczbą jest i ją wstawić. Natomiast nie staramy się wyznaczyć -a, bo on ma tam być (wyjątkiem jest funkcja stała, ale w tego typu zadaniach się z nią nie spotkasz).
Po drugie: do wyznaczenia wzoru potrzebujemy tylu punktów, ile mamy niewiadomych we wzorze (są od tego wyjątki, ale one zostaną omówione w osobnym poście). Czyli jeśli mamy wzór , to do wyznaczenia wzoru potrzebujemy jednego punktu, bo mamy jedną niewiadomą: (jak mówiłam, -a nie liczymy).
Potrzebujemy jednego punktu i mamy jeden punkt: . Co z nim robimy?
Punkt ma dwie współrzędne: -ową (u nas ) i -ową (u nas ). Punkt należy do wykresu tej funkcji, więc możemy podstawić do wzoru jego współrzędne. No dobra, tylko jak to zrobić, skoro we wzorze nie mamy -a? Oznaczenia oraz możemy stosować zamiennie, czyli nasz wzór możemy zapisać tak:
Podstawiamy w miejsce -a i w miejsce -a.
Otrzymaliśmy równanie, w którym niewiadomą jest . Chcemy ją wyznaczyć (o rozwiązywaniu równań możesz poczytać tu).
Wyznaczyliśmy , teraz wstawiamy je do wzoru.
Odpowiedź: Wzór tej funkcji to
Następne zadanie:
Dana jest funkcja (patrz rysunek). Wyznacz jej wzór.
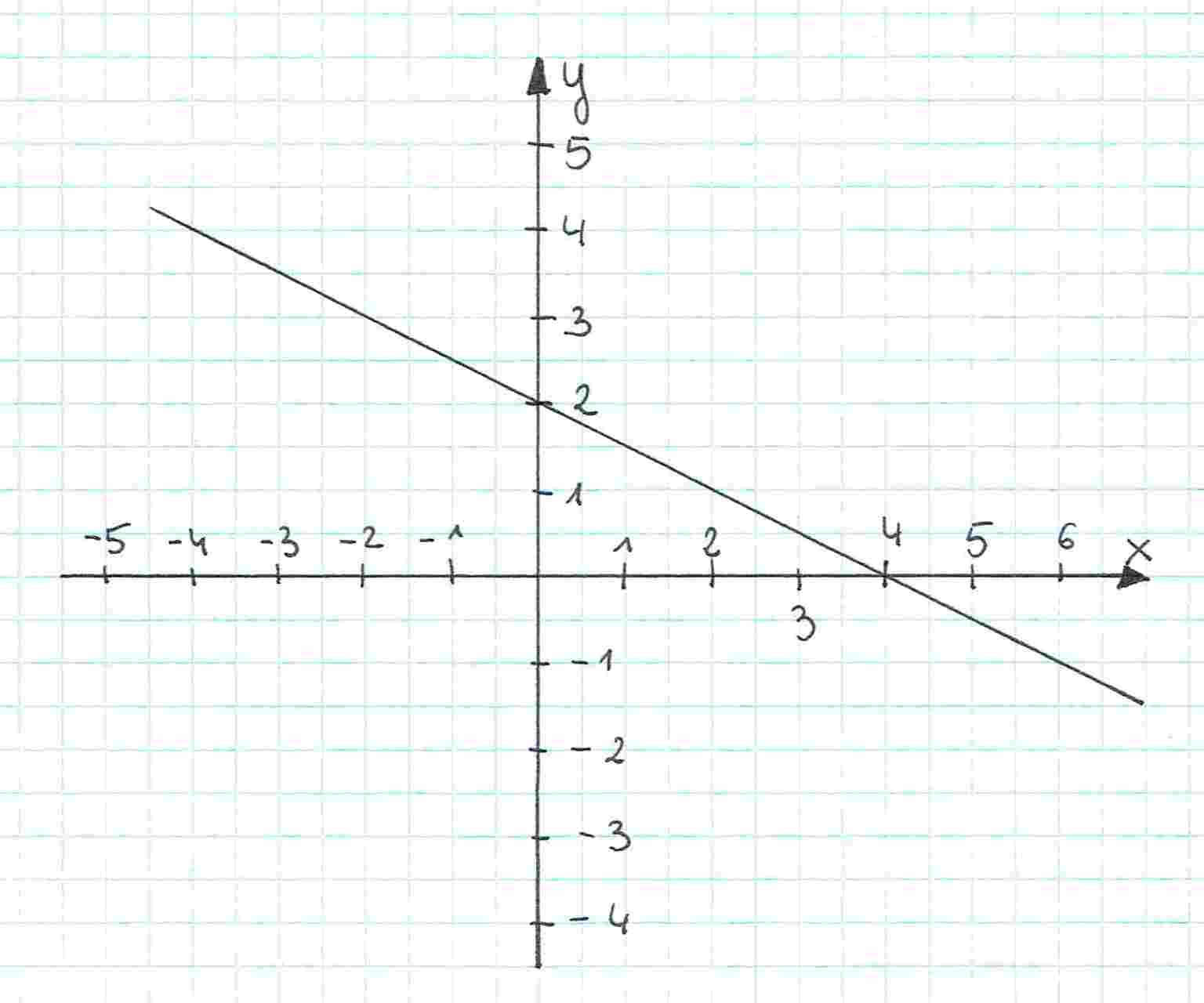
Najpierw patrzymy, ile jest niewiadomych we wzorze. Są dwie: i (nie liczymy -a, bo jego nie będziemy wyznaczać). To znaczy, że potrzebujemy dwóch punktów, które dadzą nam dwa równania. Nie mamy żadnych punktów w treści zadania, ale możemy je odczytać z wykresu. Pierwszy punkt (nazwijmy go ) ma współrzędne , a drugi (nazwijmy go ) ma współrzędne .
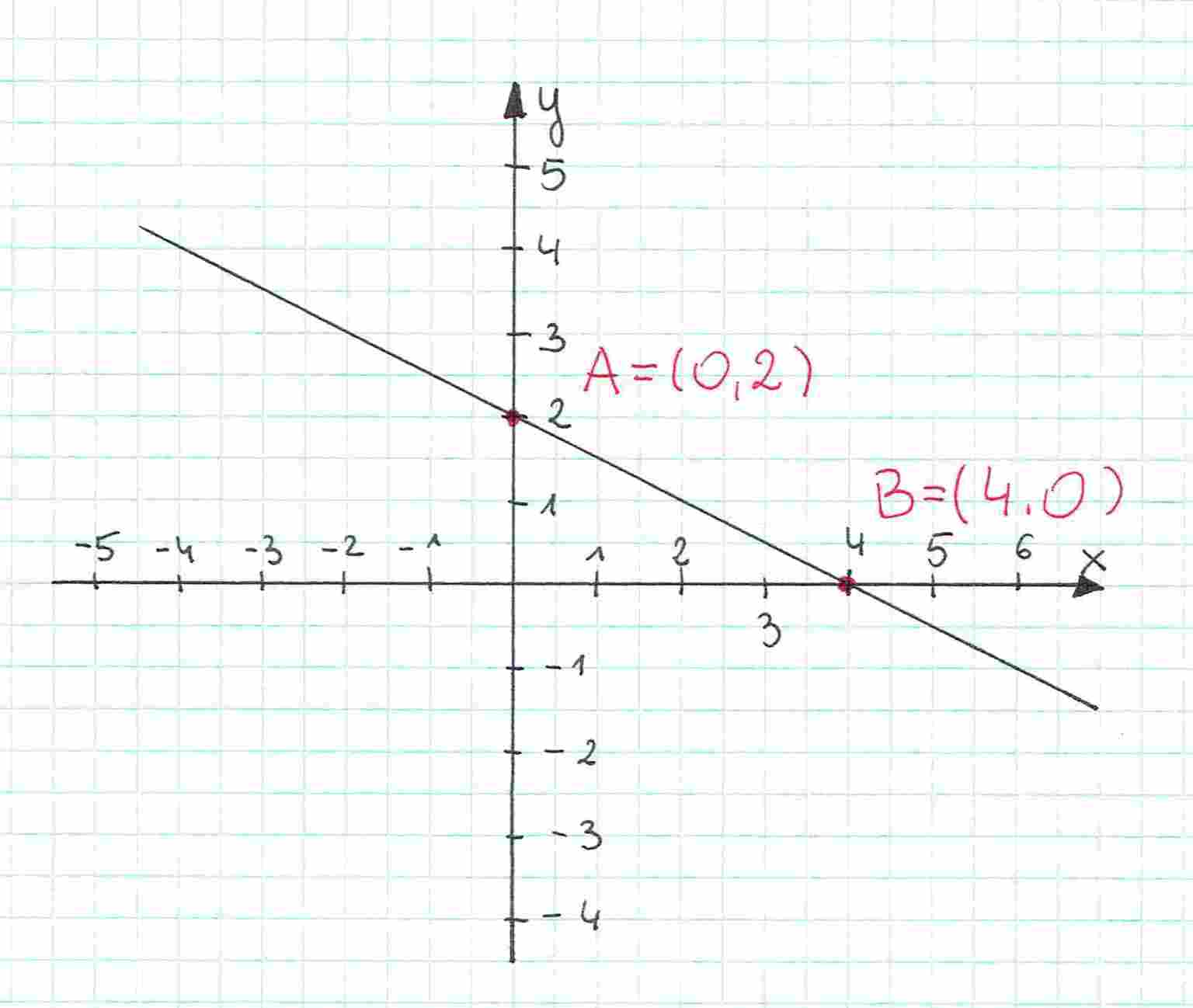
Będziemy teraz te współrzędne podstawiać do wzoru funkcji. Żeby nam się nie myliło, tak jak poprzednio zamiast zapiszemy .
Z tego samego powodu dobrze jest współrzędne punktu oznaczyć sobie malutkimi literami i , żeby nie wstawić ich odwrotnie.
Pierwsze równanie:
Drugie równanie:
Mamy dwa równania, tworzymy więc układ równań.
Wykonujemy mnożenie:
W pierwszym równaniu nam znikło i mamy już , możemy je wstawić do drugiego równania:
Rozwiązujemy drugie równanie:
Mamy już wyznaczone i , wstawiamy je do wzoru .
Odpowiedź:
________________________________
W tych dwóch zadaniach mogłeś zobaczyć dwa sposoby podania współrzędnych punktu:
- informacja, że "do wykresu funkcji należy punkt ",
- punkt zaznaczony jest na wykresie (wtedy odczytujemy jego współrzędne).
Są to sposoby, z którymi większość osób dobrze sobie radzi. Niestety, nie są one jedyne. Współrzędne punktu mogą być podane również tak:
- "wiadomo, że " - taki zapis oznacza, że , a , czyli , czyli dostaliśmy punkt ;
- "funkcja przyjmuje wartość dla argumentu " - argument to , a wartość funkcji to , czyli mamy punkt ;
- "miejscem zerowym funkcji jest " - miejsce zerowe to taki , dla którego jest równy zero, a więc dostaliśmy punkt ;
- "funkcja przechodzi przez początek układu współrzędnych" - czyli przez punkt ;
- w przypadku funkcji kwadratowej możemy mieć w zadaniu informację, że "wierzchołek paraboli ma współrzędne " - to też jest punkt należący do wykresu;
- oraz kilka innych, bardziej skomplikowanych, którymi póki co nie będziemy się zajmować 😉
Przećwiczmy wyznaczanie wzoru funkcji w zadaniach z tymi zapisami.
Funkcja (patrz rysunek) przyjmuje wartość dla argumentu . Wyznacz wzór tej funkcji.
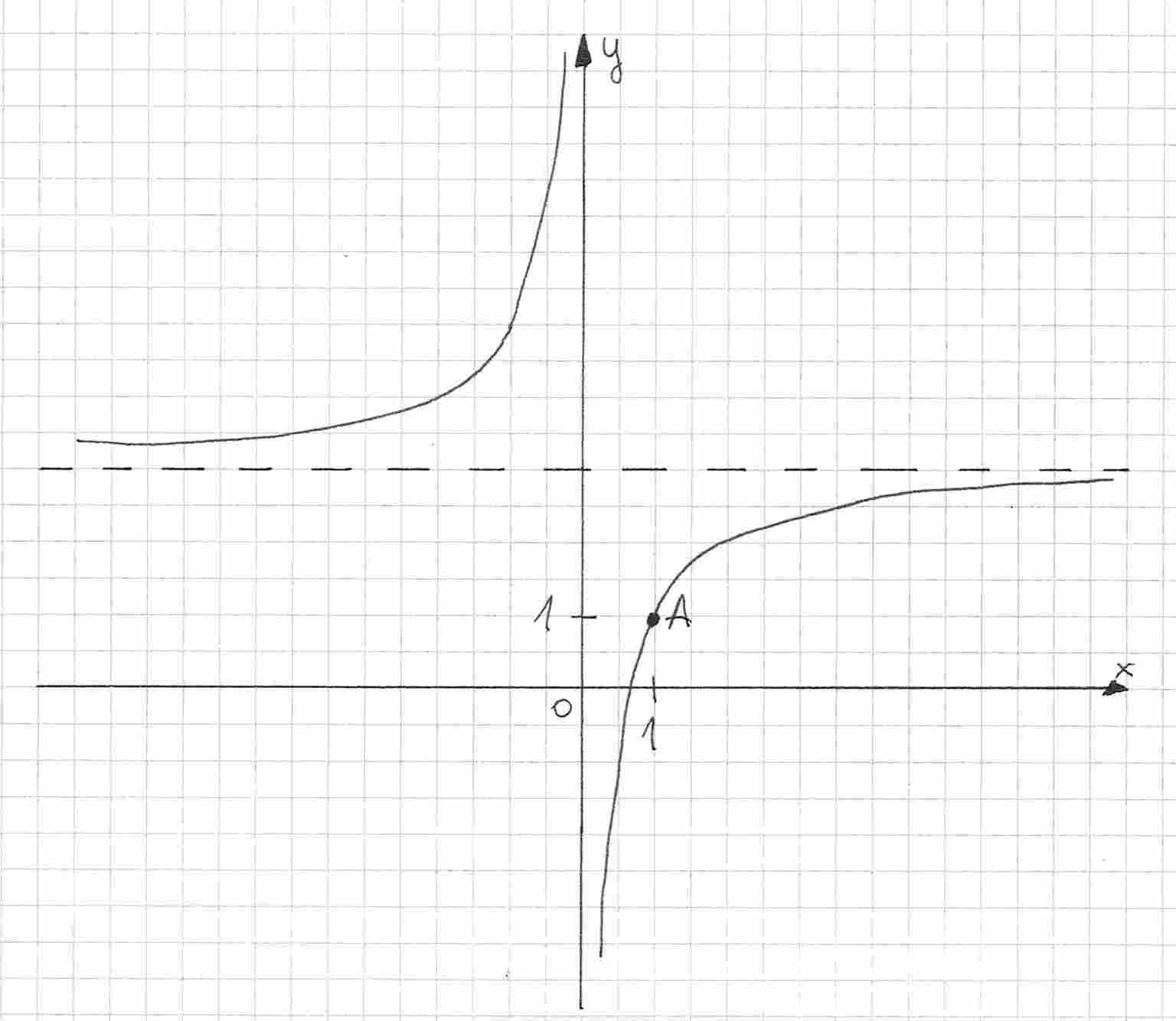
Zaczynamy od tego, że sprawdzamy, ile mamy niewiadomych. Są dwie: oraz - czyli potrzebujemy dwóch punktów. Jeden z nich możemy odczytać z rysunku: . Drugi mamy zawarty w treści zadania: "przyjmuje wartość dla argumentu " - argument to , a wartość funkcji to , mamy więc punkt Będziemy współrzędne tych dwóch punktów podstawiać do wzoru, aby otrzymać dwa równania.
W ten sposób powstały nam dwa równania na dwie niewiadome. To oznacza układ równań.
W pierwszym równaniu mogę się pozbyć ułamka, bo to po prostu . Natomiast drugie równanie pomnożę obustronnie przez , żeby zniknął ułamek.
Teraz z pierwszego równania wyznaczam .
Następnie wstawiam wyznaczone (czyli ) do drugiego równania.
Rozwiązuję drugie równanie, pierwsze zostawiając póki co bez zmian.
Wstawiam wyznaczoną wartość do pierwszego równania i wyznaczam :
Otrzymaliśmy współczynniki oraz , teraz wyznaczymy wzór. Bierzemy wzór, który mamy podany w zadaniu i wstawiamy do niego liczby.
Odpowiedź: Wzór tej funkcji to .
Kolejne zadanie:
Funkcja przechodzi przez początek układu współrzędnych, a jej wierzchołek ma współrzędne . Znajdź współczynniki i .
Zaczynamy od tego, że sprawdzamy, ile mamy niewiadomych. Są dwie ( i ), więc potrzebujemy dwóch punktów. Pierwszy z nich to punkt , natomiast drugi (nazwijmy go ) to punkt , ponieważ funkcja przechodzi przez początek układu współrzędnych. Podstawiamy współrzędne tych dwóch punktów do wzoru funkcji.
Tworzymy układ równań.
Porządkujemy nasze równania. Zaczynam od wykonania potęgowania.
Następnie wykonuję mnożenie.
Skracam ułamek w pierwszym równaniu oraz porządkuję drugie.
Jak widzisz, jeden współczynnik, czyli , już mamy. Możemy otrzymaną wartość wstawić do pierwszego równania.
Zajmijmy się teraz pierwszym równaniem. Ułamki utrudniają sprawę, więc pomnożymy równanie przez ich wspólny mianownik (czyli przez ), żeby się poskracały.
Pierwsze równanie wygląda już przyzwoicie, więc możemy z niego wyznaczyć .
Mamy nasze współczynniki. Zwróć uwagę, że tym razem polecenie nie brzmiało "wyznacz wzór funkcji", tylko "znajdź współczynniki i " - czyli już nic nie musimy robić.
Odpowiedź: Szukane współczynniki to oraz .
Do tej pory w zadaniach mieliśmy podany wzór funkcji. Nie zawsze jednak musi tak być. Zadanie może wyglądać też tak:
Wyznacz wzór funkcji liniowej , takiej, że , a jej miejscem zerowym jest .
Jak widzisz, nie mamy tu podanego wzoru funkcji. Wiemy natomiast, że jest to funkcja liniowa. Twoim zadaniem jest wiedzieć, że wzór funkcji liniowej wygląda tak: . Mamy dwie niewiadome, czyli potrzebujemy dwóch punktów.
Pierwszy punkt mamy z informacji, że . to współrzędna -owa, a to współrzędna -owa, więc mamy punkt . Drugi punkt mamy z informacji, że miejscem zerowym funkcji jest . Miejsce zerowe to taki , dla którego jest zero - mamy więc punkt . Możemy teraz podstawić współrzędne do wzoru.
Mamy dwa równania, tworzymy układ równań.
Wyłączam z drugiego rówania (bo tam będzie to prostsze).
Wstawiam w miejsce do pierwszego równania.
Rozwiązuję pierwsze równanie.
Wstawiam teraz w miejsce do drugiego równania.
W zadaniu chcą od nas, żebyśmy wyznaczyli wzór - czyli wstawiamy otrzymane współczynniki do wzoru.
Odpowiedź: Funkcja ma wzór .
Czasem może być tak, że równania są mniej "standardowe", jak na przykład tutaj.
Dana jest funkcja . Punkt należy do wykresu tej funkcji. Wyznacz jej wzór.
Działamy tak samo, jak zwykle. Zaczynamy od tego, że sprawdzamy, ile mamy niewiadomych we wzorze (poza -em). Mamy jedną niewiadomą - . To znaczy, że potrzebujemy jednego punktu. I ten punkt mamy: . Podstawiamy współrzędne do wzoru.
Dostaliśmy równanie na . Zastanówmy się teraz, jakie musi być , żeby to równanie było prawdziwe. Jaka liczba, podniesiona do trzeciej potęgi, da nam osiem? Jest to dwa.
To znaczy, że . Wracamy do polecenia: "Wyznacz jej wzór." Wstawiamy nasze do wzoru.
Odpowiedź: Wzór tej funkcji to .
Teraz zadanie dla Ciebie. Powodzenia 🙂 Oczywiście w razie problemów pytaj w komentarzu.
Dana jest funkcja kwadratowa , taka, że . Funkcja ta dla argumentu przyjmuje wartość . Wyznacz .
Odpowiedź: