Spis treści
- Wzór na współrzędne środka odcinka
- Wyznaczanie środka odcinka
- Zadania z wykorzystaniem wzoru na środek odcinka
Wzór na współrzędne środka odcinka
Jeśli mamy odcinek o końcach w punktach oraz , to środek tego odcinka będzie miał współrzędne
Wyznaczanie środka odcinka
Jeśli chodzi o zadania z wykorzystaniem tego wzoru, to w optymistycznej wersji dostaniemy współrzędne końców odcinka i polecenie, by znaleźć środek tego odcinka - czyli bezpośrednio podstawić do wzoru. Może ono wyglądać na przykład tak:
Mamy znaleźć środek odcinka, mamy podane współrzędne jego końców. W takiej sytuacji po prostu podstawiamy liczby do tego wzoru:
Wszędzie tam, gdzie w grę wchodzą współrzędne, bardzo łatwo jest się pomylić i wpisać w miejsce współrzędnej -owej współrzędną -ową lub odwrotnie. Fajny sposób podpatrzyłam u mojej uczennicy, która wypisywała sobie punkty jeden pod drugim i nad każdą współrzędną pisała lub , o w taki sposób:
Dzięki temu dużo trudniej jest się pomylić, zwłaszcza w sytuacji, gdy się spieszymy.
W ten sposób obliczyliśmy współrzędne środka odcinka. Możesz zobaczyć, jak wygląda to na rysunku:
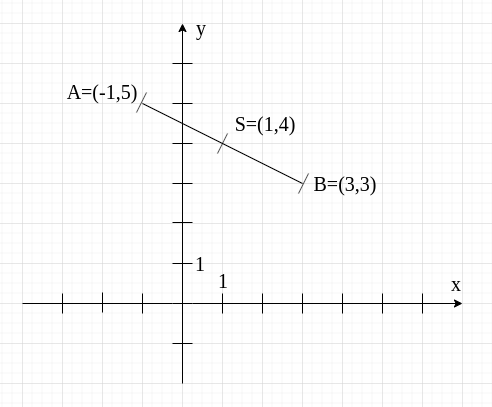
Należy pamiętać, że litery , oraz są oczywiście umowne - punkty mogą być nazwane inaczej. Tak jest na przykład w tym zadaniu.
Możemy skorzystać ze standardowego wzoru
ale jest spore ryzyko, że przy podstawianiu się pomylimy, dlatego warto wzór dostosować do zadania. My mamy odcinek o środku w punkcie .
Wypisujemy sobie punkty i oznaczamy współrzędne jako i :
Podstawiamy współrzędne do wzoru:
Wykonujemy po kolei działania:
Zadania z wykorzystaniem wzoru na środek odcinka
Trochę trudniejszy wariant zadania wygląda tak, że mamy podane współrzędne środka i jednego końca odcinka, a musimy znaleźć drugi koniec. Tu mamy przykład takiego zadania.
Zacznijmy od dostosowania naszego wzoru i podstawienia współrzędnych.
Teraz skorzystamy z tego, że znamy współrzędne punktu . Skoro , to do naszego wzoru zamiast mogę wstawić .
Znaleźliśmy się w sytuacji, w której mamy dwie niewadome - to znaczy, że potrzebujemy dwóch równań. Aby je otrzymać, wystarczy, że z naszego wyrażenia oddzielimy sobie współrzędne.
Wiemy, że -owa współrzędna odcinka to . Jednocześnie wiemy, że jest ona równa . Stąd:
Dokładnie tak samo możemy zrobić z -ową współrzędną:
Otrzymaliśmy dwa równania, z których możemy wyznaczyć i . Zajmę się teraz pierwszym równaniem.
Zacznę od pozbycia się ułamka, mnożąc równanie obustronnie przez .
Wykonuję mnożenie po lewej stronie.
Przerzucam -y na lewo, a liczby na prawo.
Wykonuję działanie po prawej stronie.
Aby otrzymać , a nie , mnożę obustronnie przez .
Mamy już pierwszą współrzędną punktu . Teraz analogicznie wyznaczymy drugą.
Jeśli któryś krok był dla Ciebie niezrozumiały, to tutaj możesz poczytać o rozwiązywaniu równań.
Mamy współrzędne oraz , możemy więc zapisać, że
Może nam się trafić też takie zadanie, że mamy podane wszystkie trzy punkty (końce odcinka oraz jego środek), ale we współrzędnych są niewiadome. Tu możesz zobaczyć przykład takiego zadania:
Podobnie jak poprzednio, zapisujemy wzór na środek odcinka i podstawiamy do niego nasze współrzędne. Punkt jest środkiem odcinka , więc wzór wygląda tak:
Wiemy, że , dlatego
Tak jak poprzednio, mamy dwie niewiadome, więc potrzebujemy dwóch równań. Zapewnią nam je dwie współrzędne punktu.
Pierwsze równanie wygląda tak:
Rozwiążmy je:
Teraz drugie równanie:
Rozwiązujemy:
Naszym zadaniem było wyznaczenie i , więc nie musimy nic więcej robić.
Do tej pory było o tyle łatwo, że było dla nas jasne, że mamy skorzystać ze wzoru na środek odcinka. Może nam się jednak trafić bardziej złożone zadanie, w którym skorzystanie z tego wzoru nie da nam gotowego rozwiązania, a jedynie będzie jednym z etapów. Co więcej, wyrażenie "środek odcinka" może w ogóle nie pojawić się w treści zadania i sami musimy się zorientować, że nas ten środek obchodzi. Tak będzie w tym zadaniu:
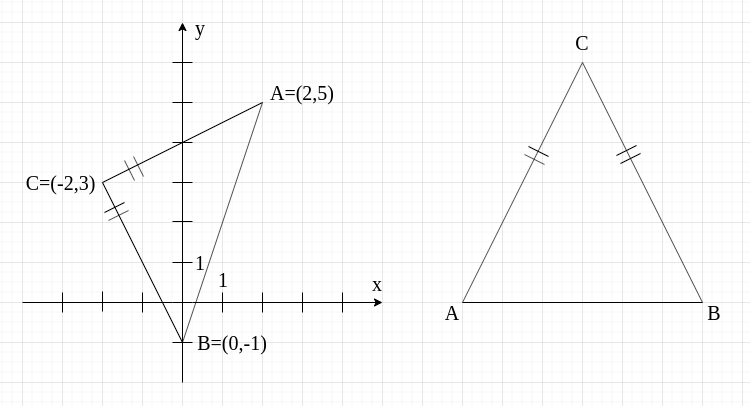
Zacznijmy od zrobienia rysunku pomocniczego. Możemy zrobić dokładny rysunek nanosząc te punkty na układ współrzędnych albo po prostu "na oko" narysować sobie trójkąt równoramienny. Ja zrobię rysunek na oba sposoby, a Ty samodzielnie zdecyduj, który wolisz 🙂
Najpierw naniosę na rysunek to, co wiemy z zadania, czyli punkty oraz informację, że boki i mają tę samą długość.
Mamy wyznaczyć długość wysokości opuszczonej z wierzchołka . Zaznaczę ją na rysunku.
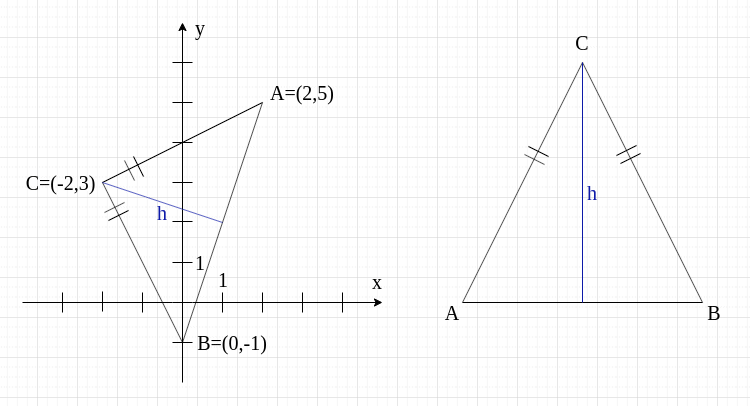
Punkt, w którym wysokość dzieli podstawę, oznaczę sobie jako .
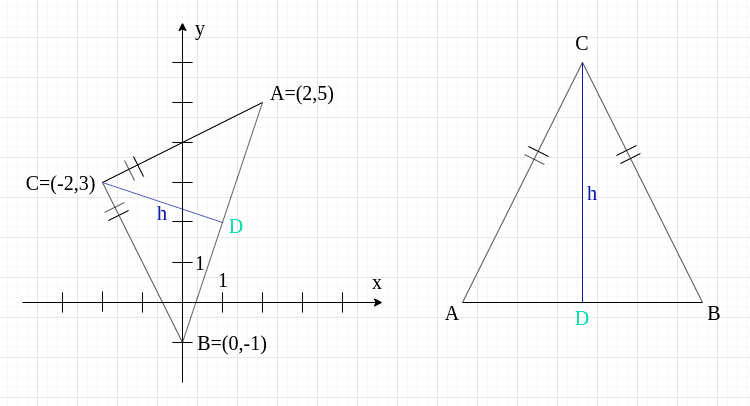
I teraz tak: trójkąt równoramienny ma taką własność, że jego wysokość dzieli podstawę na połowy - a to oznacza, że punkt jest środkiem odcinka . Możemy więc wyznaczyć ze wzoru na środek odcinka współrzędne tego punktu.
No dobra, tylko po co nam ten punkt ? Wróćmy do rysunku. Możesz na nim zobaczyć, że wysokość, którą mamy obliczyć, to odcinek - a na długość odcinka mamy wzór:
Pierwiastka z liczby nie ma, możemy sprawdzić, czy da się coś wyciągnąć przed pierwiastek:
Niestety nic się nie powtarza, więc zostaje (jeśli nie wiesz, o co chodzi, to tutaj możesz poczytać o wyłączaniu czynnika przed pierwiastek).
Jeśli mamy odcinek o końcach w punktach oraz , to środek tego odcinka będzie miał współrzędne
Przykład: odcinek o końcach w punktach oraz będzie miał środek w punkcie
Wzór warto dostosować do tego, jakie mamy punkty.
Przykład: Jeśli mamy odcinek o końcach w punktach oraz , a mamy wyznaczyć punkt będący środkiem odcinka, to wzór będzie wyglądał tak:
Jeśli mamy podany środek i jeden z końców, to korzystając ze wzoru możemy wyznaczyć drugi koniec. Podstawiamy do wzoru współrzędne, które mamy, a następnie układamy dwa równania.
Przykład: Jeśli mamy odcinek o środku w punkcie i jednym z końców w punkcie , to
Możemy ułożyć dwa równania:
Rozwiązując równania otrzymamy współrzędne punktu :
Często wyznaczenie środka odcinka jest konieczne do rozwiązania bardziej złożonego zadania z geometrii analitycznej. Jeśli przy takim zadaniu kompletnie nie wiesz, za co się zabrać, a masz podane dwa punkty, to zawsze możesz wyznaczyć środek odcinka - a nuż się przyda 😉
Rozwiązywanie równań liniowych