Spis treści:
- Symbol średniej
- Jak obliczyć średnią arytmetyczną?
- Obliczanie średniej arytmetycznej - trudniejsze przypadki
- Zadania z wykorzystaniem średniej arytmetycznej
Symbol średniej
Jak obliczyć średnią arytmetyczną?
Jeśli mamy liczb , to ich średnia arytmetyczna jest równa
No nie wygląda to zbyt dobrze, ale zaraz na przykładzie pokażę Ci, jak to rozumieć.
W tym miejscu chciałabym wspomnieć, że we wzorze na średnią litera jest umowna - tutaj na przykład mamy podane masy, więc wzór będzie wyglądał tak:
Litera mówi nam, ile mamy liczb, z których chcemy policzyć średnią. W naszym zadaniu mamy dane masy pięciu kotów, więc u nas jest równe . Możemy więc od razu dostosować nasz wzór.
Litery , , , i to kolejne liczby, z których liczymy średnią. U nas są to kolejne masy kotów: czyli kg, kg itd. Wstawmy to do wzoru:
[kg]
Odpowiedź: Średnia waga kota to kg.
Obliczanie średniej arytmetycznej - trudniejsze przypadki
Gdy mamy po prostu wypisane liczby i musimy obliczyć ich średnią, to nie jest to skomplikowane. Nieco trudniejsza jest taka sytuacja:
Jest to niestety czasochłonna metoda. Musimy zdać sobie sprawę z tego, że gdybyśmy mieli nie jedenaście kotów, tylko sto jedenaście, to już by nie przeszło. Dlatego pokażę Ci, jak zrobić to sprytniej:
Zamiast zapisywać , zapisaliśmy , podobnie z pozostałymi liczbami. Wynik będzie ten sam, ale liczenia znacznie mniej. Dokończmy przykład:
[kg]
Odpowiedź: Średnio kot ważył kg.
Ten sposób zapisu będziemy wykorzystywać głównie tam, gdzie dane są przedstawione w tabeli czy na wykresie. Tak będzie w następnym zadaniu:
| Wzrost [cm] | Liczba uczestników |
Sporo osób zastanawia się, z której kolumny tabeli wziąć liczby do średniej. Ponieważ mamy obliczyć średni wzrost uczestników, to właśnie wzrost będziemy sumować na górze. Musimy pamiętać o tym, że wyniki się powtarzają: liczby, z których liczymy średnią, to nie
tylko
I znowu, można dodawać te wszystkie liczby na piechotę, ale można to też zrobić szybciej, zapisując np: zamiast
[cm]
Odpowiedź: Średni wzrost uczestnika to cm.
Teraz przećwiczymy liczenie średniej zestawu danych przedstawionych na diagramie - to zazwyczaj jest najmniej intuicyjne dla większości osób.
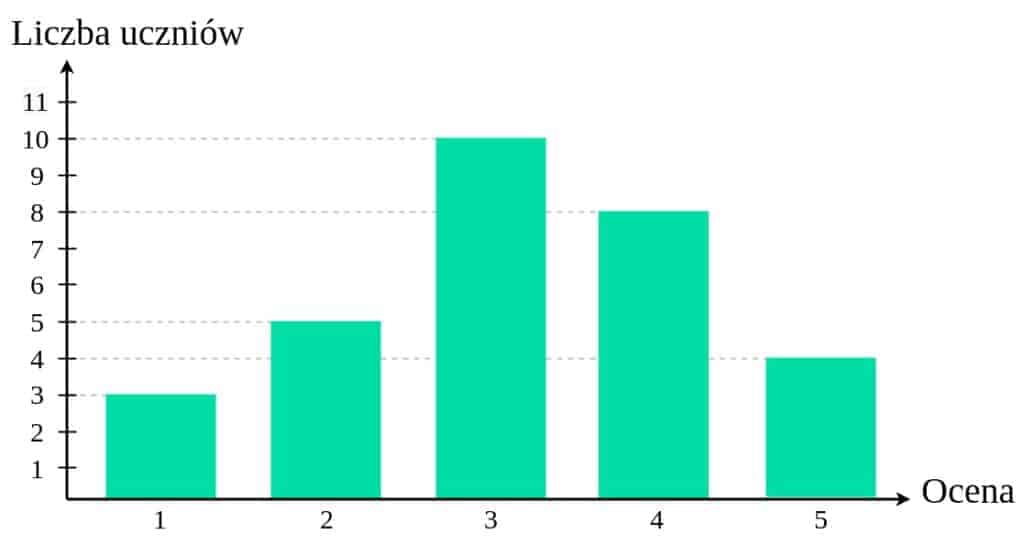
Na wstępie należy się zastanowić, z czego liczymy średnią. Pytają nas o średnią ocenę, więc to oceny są liczbami, z których liczymy średnią. Dla każdej oceny możemy odczytać, ile osób ją otrzymało (a więc ile razy się powtarza). Nasz zestaw danych wygląda tak (pokażę Ci tylko początek, bo tu już mamy za dużo liczb):
Policzymy teraz średnią. Ponieważ na ocenę nie mamy zarezerwowanej żadnej konkretnej litery (jak w przypadku wysokości czy masy), oznaczę ją po prostu jako .
Odpowiedź: W tej klasie uczniowie średnio uzyskali ocenę .
Zadania z wykorzystaniem średniej arytmetycznej
Do tej pory mieliśmy za zadanie obliczyć średnią. Może nam się jednak trafić zadanie, w którym mamy podaną średnią, a nie mamy części danych na tę średnią się składających. Zadanie może wyglądać na przykład tak:
W takiej sytuacji układamy równanie, korzystając ze wzoru na średnią:
W mianowniku wpisałam liczbę , bo tyle mamy liczb w zbiorze, zaś w liczniku dodałam do siebie te liczby. Po prawej stronie wpisałam wynik tego działania, czyli średnią. Teraz musimy to równanie po prostu rozwiązać. Pierwsze, co chcemy zrobić, to pozbyć się ułamka. Robimy to, mnożąc obustronnie równanie przez .
Dzięki temu ułamek nam się skróci.
Wykonujemy mnożenie po prawej stronie i dodawanie po lewej:
Przerzucamy na drugą stronę:
Jeśli któryś krok nie był dla Ciebie zrozumiały, to tutaj możesz poczytać o rozwiązywaniu równań.
Podobne, ale nieco trudniejsze zadanie, może wyglądać tak:
Ponownie będziemy korzystać ze wzoru na średnią. Wszystkich zeszytów łącznie jest , natomiast suma liczb, których średnią liczymy, to . Stąd średnia jest równa
Mamy równanie do rozwiązania. Trochę je uporządkujmy:
Teraz pozbędę się ułamka, mnożąc obustronnie przez - pamiętajmy o nawiasach!
Skracamy:
Teraz wykonuję mnożenie po prawej stronie:
Przerzucam liczby na prawą stronę, a na lewą:
Dzielę obustronnie przez to, co stoi przy , czyli :
Odpowiedź: Krystyna ma zeszytów.
Ostatnie zadanie, które chcę Ci dziś pokazać, jest o tyle skomplikowane, że mamy w nim dużo niewiadomych, z którymi nie wiadomo za bardzo, co zrobić.
Zacznijmy od ułożenia równania. Wiemy, że w drużynie są cztery osoby, których średnia wzrostu wynosi cm. Na podstawie tej informacji możemy ułożyć takie równanie:
Przez i oznaczyłam wzrost zawodników, bo nie wiemy, ile mierzy każdy z nich. I uwaga - nie musimy wiedzieć! Nas interesuje tylko wzrost trenera, który oznaczę jako . Średnia uwzględniająca trenera wygląda tak:
Po pierwsze, dodałam wzrost trenera. Zmieniłam wielkość średniej, która po uwzględnieniu trenera wzrosła. Zmieniłam też liczbę w mianowniku, bo po uwzględnieniu trenera mamy osób, a nie .
Teraz tak: ewidentnie zawadzają nam niewiadome i . Wiele osób kombinuje, jak obliczyć każdą z tych wielkości, a wcale nie musimy tego robić. Możemy obliczyć całe wyrażenie . Aby to zrobić, wykorzystamy pierwsze równanie.
Pomnożę je obustronnie przez , aby pozbyć się ułamka.
Skracamy:
Wykonujemy mnożenie po prawej stronie:
Spójrz, co się stało: wyznaczyliśmy wartość wyrażenia , mimo że nie wiemy, ile wynosi każda wielkość z osobna. Teraz możemy wstawić to do drugiego równania.
Tym sposobem zamiast pięciu niewiadomych mamy jedną, którą teraz możemy wyznaczyć. Na początek pozbędę się ułamka.
Wykonuję mnożenie po prawej stronie.
Przerzucam na prawą stronę.
[cm]
Mieliśmy obliczyć wzrost trenera, dlatego nic już więcej nie musimy robić.
Odpowiedź: Wzrost trenera wynosi cm.
Symbol średniej to pionowa kreska na górze.
Przykład: średnią masę oznaczymy jako .
Jeśli mamy liczb , to ich średnia arytmetyczna jest równa
Przykład: średnia liczb to .
Jeśli dane się powtarzają, to uwzględniamy to przy wyznaczaniu średniej.
Przykład: jeśli wiemy, że cztery koty miały masę kg, pięć ważyło kg, a dwa ważyły kg, to średnia masa kota jest równa .
Jeśli dane przedstawione są w tabeli czy na diagramie, możemy napotkać na następujące trudności:
- często nie wiemy, z której rubryki wziąć liczby do średniej - w takiej sytuacji musimy zadać sobie pytanie, czego średnią liczymy, np. jeśli mamy obliczyć średni wzrost, to kierujemy się do rubryki oznaczonej jako wzrost;
- musimy pamiętać, że liczby podane w tabeli się powtarzają i uwzględnić to podczas obliczania średniej - z tabeli możemy odczytać, ile razy powtarza się każda liczba.
Przykład: jeśli mamy dane przedstawione w taki sposób
| Wzrost [cm] | ||||
| Liczba uczestników |
to średni wzrost uczestnika wynosi .
Jeśli w zadaniu mamy podaną średnią, to korzystając ze wzoru na średnią układamy równanie i je rozwiązujemy.
Przykład: jeśli wiemy, że średnia arytmetyczna zbioru liczb wynosi , to ułożymy równanie
Rozwiązywanie równań liniowych