Spis treści
- Wzór funkcji liniowej
- Przykłady funkcji liniowej
- Wykres funkcji liniowej
- Miejsce zerowe funkcji liniowej
- Znaczenie współczynników we wzorze funkcji liniowej
- Monotoniczność funkcji liniowej
- Trudniejsze przypadki
Wzór funkcji liniowej
Funkcja liniowa określona jest wzorem
Może być też zapisana tak:
W tym wzorze współczynniki oraz mogą być dowolnymi liczbami.
Przykłady funkcji liniowej
Każda funkcja, która jest postaci , jest funkcją liniową. Poniżej możesz zobaczyć przykłady wzorów takiej funkcji:
Wszystkie dalsze zagadnienia związane z funkcją liniową omówię na przykładzie tych dwóch funkcji.
Wykres funkcji liniowej
Zacznijmy od pierwszej funkcji.
Aby znaleźć potrzebne nam punkty, zrobimy sobie tabelkę.
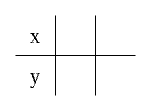
W wierszu wstawiamy dwie dowolne liczby. Warto wybrać takie, które będą proste w rachunkach, na przykład i .
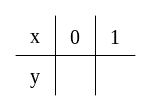
I teraz tak: bierzemy wzór naszej funkcji i w miejsce -a podstawiamy wybrane przez nas wartości.
Nasza funkcja ma wzór . Żeby nam się nie myliło, możemy ją sobie zapisać w postaci . W miejsce -a wstawiamy pierwszą wybraną przez nas wartość, czyli .
Otrzymaną wartość wpisujemy do tabeli pod zerem.
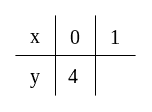
Teraz w miejsce -a podstawiam drugą wybraną przez nas wartość, czyli .
Wynik wpisujemy do tabeli pod jedynką.
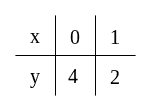
Otrzymaliśmy dwa punkty należące do naszej funkcji:
Zaznaczamy je w układzie współrzędnych.
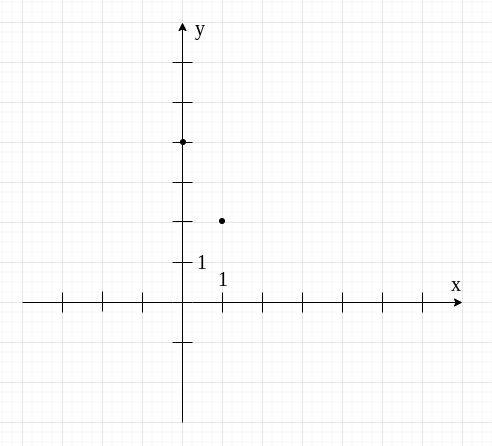
Teraz łączymy punkty prostą linią.
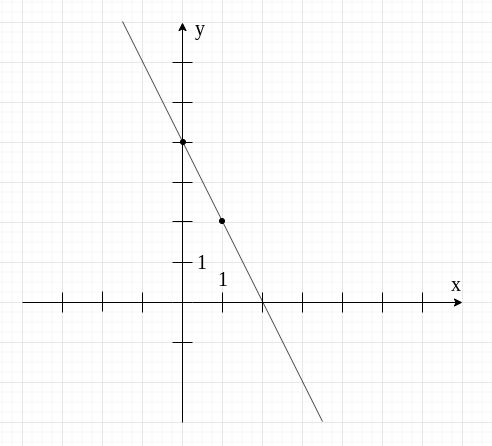
Ta prosta linia, którą otrzymaliśmy, to wykres funkcji .
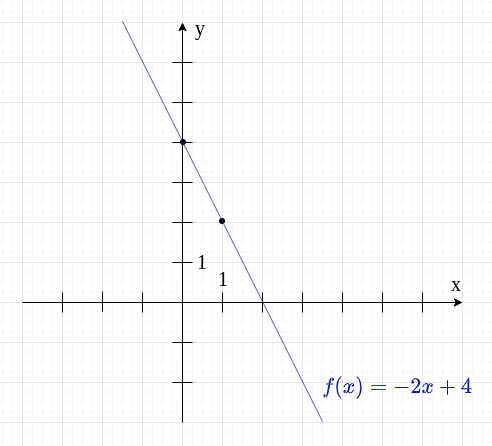
Niektóre osoby mają problem z narysowaniem prostej linii na podstawie jedynie dwóch punktów. W takiej sytuacji możemy już bez tabelki zaznaczyć dodatkowe punkty. Najpierw patrzymy, jaką "drogę" musimy pokonać między dwoma zaznaczonymi punktami.
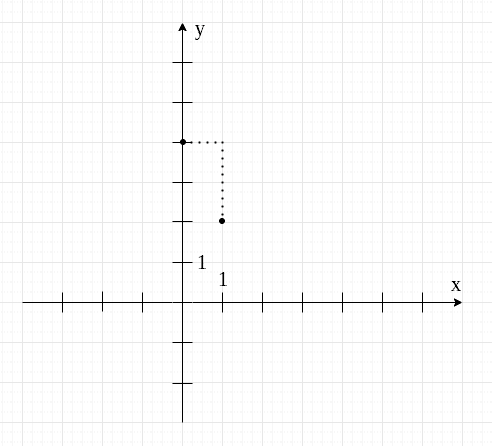
Żeby przejść od jednego punktu do drugiego musimy przemieścić się o jedną kratkę w prawo i dwie w dół. W ten sam sposób możemy przejść do następnych punktów.
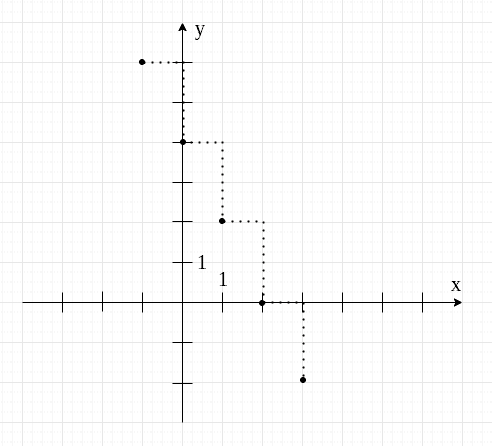
Mając ich więcej, łatwiej jest narysować prostą linię 🙂
Teraz drugi wykres.
Najpierw robię tabelkę. Ponownie wybieram sobie dwie wartości -a, oraz (pamiętaj, że możemy wybrać też inne liczby, po prostu te dwie prawie zawsze są najmniej kłopotliwe w rachunkach).
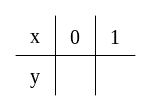
Teraz wybrane przez nas wartości podstawiamy do wzoru funkcji.
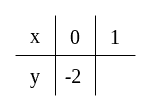
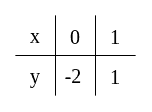
W ten sposób otrzymaliśmy dwa punkty:
Zaznaczamy te punkty w układzie współrzędnych.
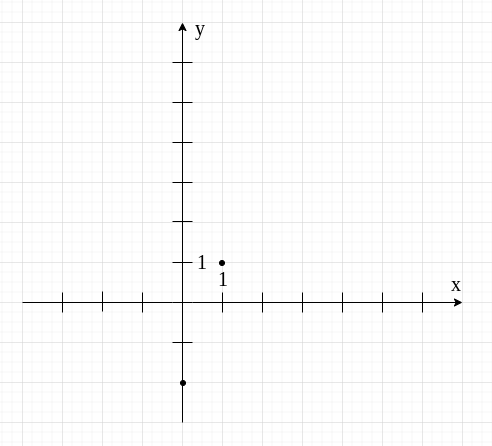
Łączymy zaznaczone punkty.
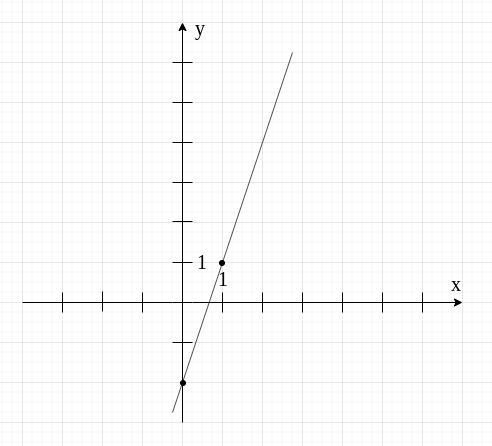
Otrzymana prosta to wykres funkcji .
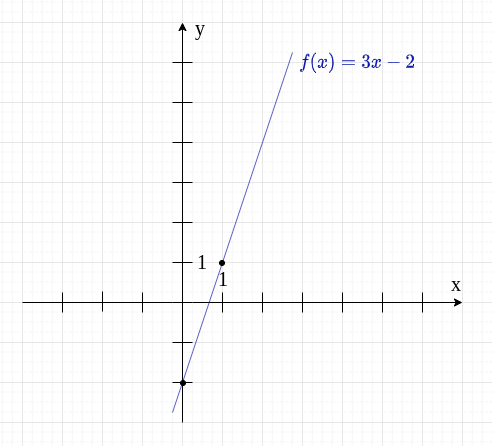
I znowu, jeśli dwa punkty to dla nas za mało, możemy zaznaczyć ich więcej. Najpierw patrzymy, jaką drogę musimy pokonać od jednego punktu do drugiego.
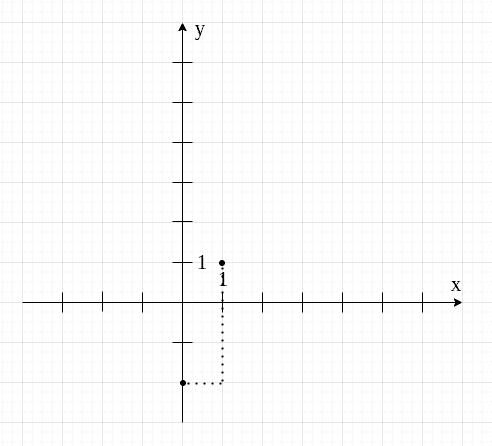
U nas jest to jedna kratka w prawo i trzy w górę. Następnie tę drogę powtarzamy, zaznaczając kolejne punkty.
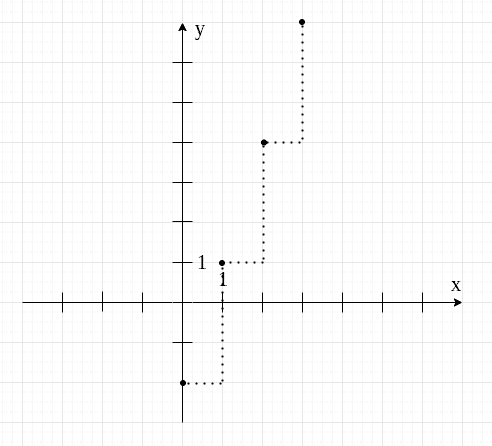
Tak na marginesie - metoda tabelki sprawdza się nie tylko przy funkcji liniowej, ale też przy wszystkich innych funkcjach (z tą różnicą, że przy innych funkcjach potrzebujemy więcej niż dwa punkty).
Znaczenie współczynników we wzorze funkcji liniowej
Funkcja liniowa jest postaci . Mamy tu dwa współczynniki: oraz .
Najpierw omówię współczynnik .
Oś to pionowa oś, na której mamy wartości -ów. Z kolei oś to pozioma oś, na której mamy wartości -ów. Przy literach i stoi wielka litera O (jak Ola), nie zero. Czytamy to następująco:
- oś - "oś o iks"
- oś - "oś o igrek".
Zobaczmy to na przykładach.
Współczynnik to ta liczba we wzorze funkcji, przy której nie stoi . W tym przypadku jest to .
I teraz tak: punkt przecięcia z osią to , czyli dla naszej funkcji będzie to . Możesz to zobaczyć na rysunku.
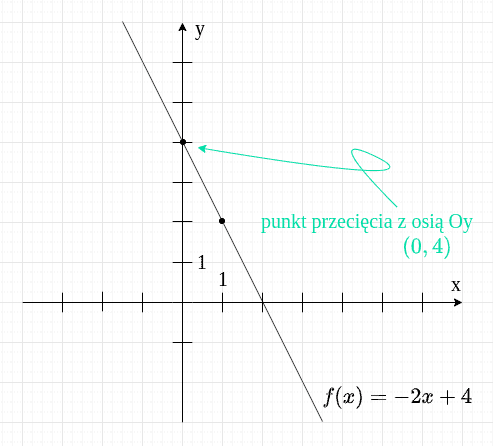
Teraz druga funkcja.
Szukamy współczynnika , czyli liczby, przy której nie stoi . U nas będzie to .
Możesz zauważyć, że we wzorze przed stoi plus, a we wzorze naszej funkcji tego plusa nie ma. Wynika to po prostu z uproszczenia. Możemy nasz wzór zapisać tak:
i wtedy wszystko się zgadza 🙂
Skoro , to punkt przecięcia z osią to u nas .
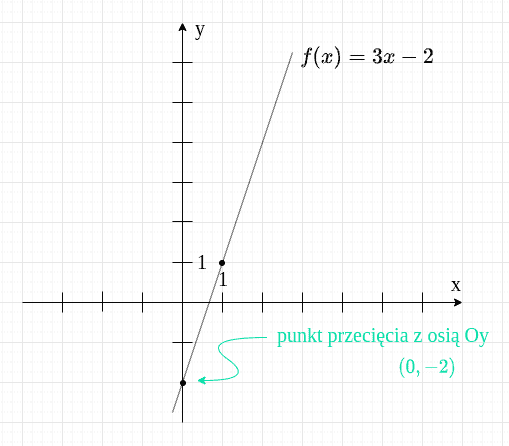
Może nam się trafić funkcja liniowa, która jest postaci , na przykład taka:
Czy taka funkcja nie ma wyrazu wolnego? Ma - jest on równy zero, tylko po prostu tego zera nie zapisujemy (tak samo jak nie mówimy, że mamy dwie gruszki i zero jabłek, tylko po prostu mamy dwie gruszki).
W takiej sytuacji wykres funkcji przecina oś w punkcie , czyli - jest to jednocześnie punkt przecięcia tej funkcji z osią .
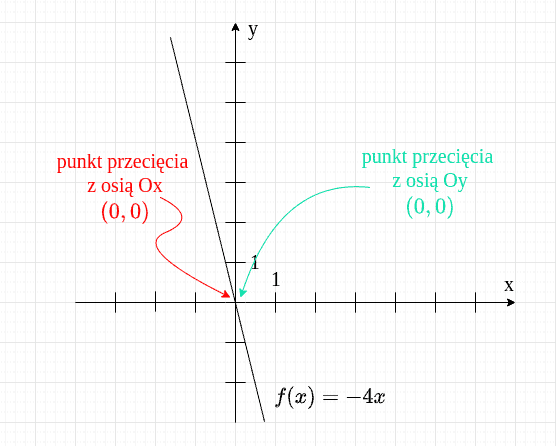
Przejdźmy do drugiego współczynnika.
I tu przechodzimy do następnego tematu.
Monotoniczność funkcji liniowej
Zobaczmy to na przykładach:
Współczynnik kierunkowy to to, co stoi przy -ie. W tym przypadku jest on równy .
Współczynnik jest ujemny, a to znaczy, że funkcja jest malejąca (czyli patrząc od lewej strony do prawej, idzie do dołu). Na wykresie możesz zobaczyć, że faktycznie tak jest.
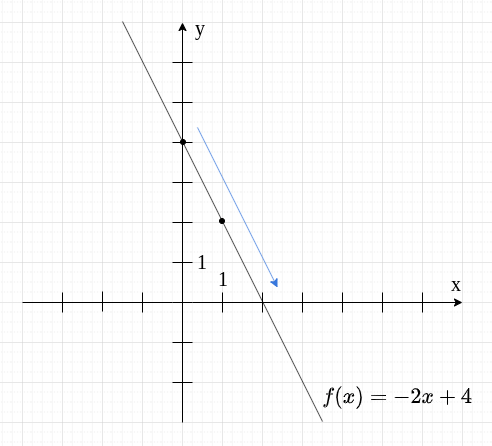
Teraz druga funkcja.
Tutaj współczynnik kierunkowy jest równy .
Jest to liczba dodatnia, więc wiemy, że funkcja jest rosnąca.
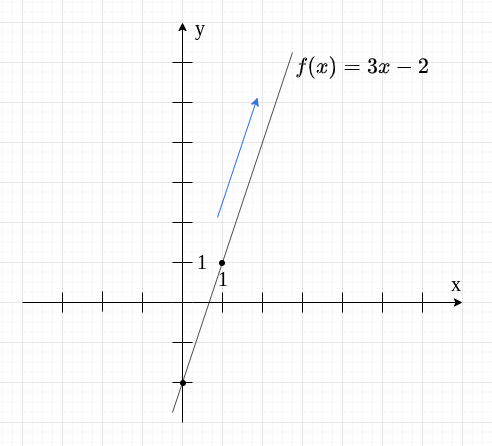
Możemy mieć jeszcze trzeci przypadek - funkcję stałą.
Funkcja stała może wyglądać na przykład tak:
Nie widzimy tu współczynnika , ale tak naprawdę jest on równy zero (tylko tego zera nie zapisujemy, bo nie ma sensu pisać, że mamy zero iksów).
Poniżej możesz zobaczyć, jak wygląda wykres funkcji stałej.
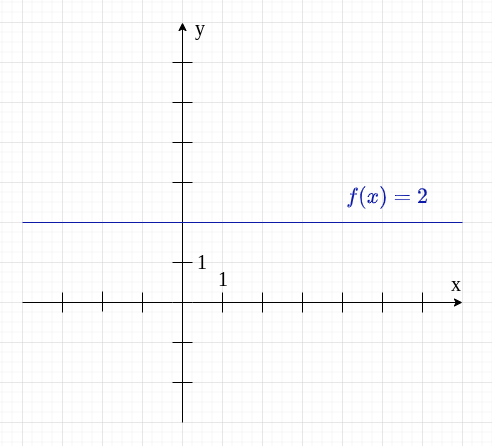
Miejsce zerowe funkcji liniowej
Pokażę Ci to na przykładach.
Aby znaleźć miejsce zerowe, bierzemy wzór funkcji i w miejsce wstawiamy zero. Robimy tak dlatego, że chcemy znaleźć taką wartość -a, dla której wartość funkcji (czyli właśnie ) jest równa .
Otrzymaliśmy równanie do rozwiązania (o rozwiązywaniu równań możesz poczytać tutaj ). Zaczynam od przerzucenia -ów na lewo.
Teraz dzielę obustronnie przez to, co stoi przy -ie, czyli przez .
Możemy skrócić czwórkę z dwójką.
Otrzymany wynik to miejsce zerowe funkcji . Zwykle miejsce zerowe oznaczamy jako .
Jak się to ma do wykresu?
Skoro u nas , to miejscem przecięcia osi będzie punkt . Na wykresie możesz zobaczyć, że faktycznie tak jest.
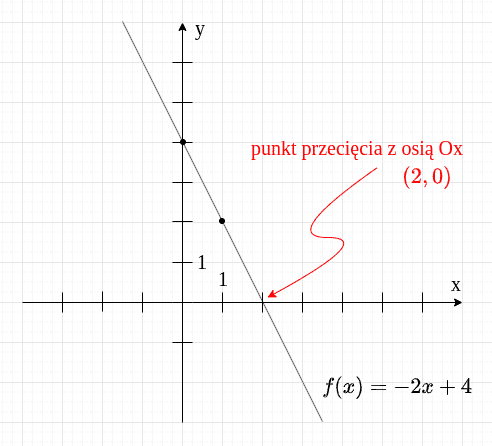
W tym miejscu dwie uwagi:
1. Nazwa "miejsce zerowe" jest myląca, bo słowo "miejsce" sugeruje punkt. Tymczasem miejsce zerowe to -owa współrzędna punktu.
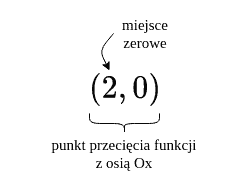
2. Mówiłam Ci, że aby wyznaczyć miejsce zerowe, w miejscu wpisujemy . Faktycznie funkcję najczęściej oznaczamy jako , ale równie dobrze może to być , czy i wtedy tam wstawiamy zero.
Teraz druga funkcja.
Sposób wyznaczania miejsca zerowego, który Ci pokazałam w poprzednim przykładzie, działa dla wszystkich rodzajów funkcji. Teraz pokażę Ci sposób, który jest szybszy, ale działa tylko dla funkcji liniowej.
Dla funkcji liniowej mamy gotowy wzór na miejsce zerowe:
My mamy funkcję , więc u nas
Dwa minusy dają nam plus.
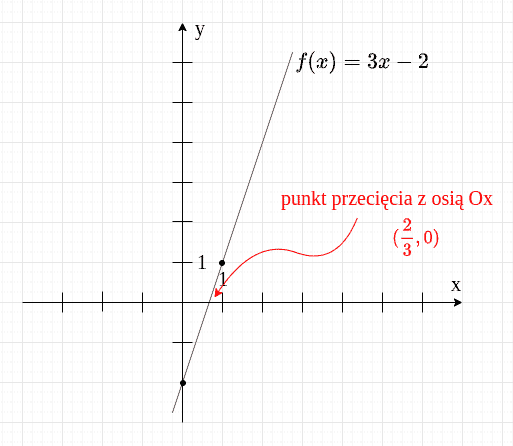
Ponieważ punkt przecięcia z osią to , możemy wywnioskować, że u nas będzie to . Możesz zobaczyć to na wykresie.
Trudniejsze przypadki
Czasem trafiają się przykłady, w których pojawia się problem przy określeniu, gdzie jest , a gdzie . Jeśli mamy taką funkcję:
to jest łatwo: , .
Ale co w takich przypadkach?
Wszystkie te przykłady to funkcja liniowa, choć może nie widać tego na pierwszy rzut oka. Pokażę Ci, jak w takich przypadkach wyznaczyć oraz .
Wiele osób popełnia taki błąd, że za bierze pierwszą liczbę (czyli ), a za drugą (czyli ). Tymczasem jest odwrotnie: to ta liczba, która stoi przy -ie. Łatwiej będzie to zobaczyć, przestawimy sobie elementy.
Tu część osób nie wie, czy jest równe , czy , czy może jedno i drugie? Współczynnik to ten kawałek funkcji, przy którym nie stoi . U nas więc .
Tu z kolei współczynnik jest "rozbudowany". Jak najbardziej może się składać z więcej niż jednej liczby.
W tym przypadku pojawia się pytanie, gdzie jest . Część osób błędnie uznaje, że skoro go nie ma to znaczy, że . Możemy łatwo rozwiązać ten problem wiedząc, że to to samo, co (tak samo jak krzesło to to samo, co jedno krzesło).
Tutaj część osób zapisuje, że . Jest to błąd. W takim przypadku wyciągamy poza ułamek i zamiast zapisujemy .
Funkcja liniowa jest postaci
Przykład: Funkcja jest funkcją liniową.
Aby narysować wykres funkcji, robimy tabelkę, do której wpisujemy wybrane przez siebie wartości -a. Następnie podstawiamy te wartości do wzoru funkcji, otrzymując w ten sposób wartości -a. Otrzymane punkty zaznaczamy w układzie współrzędnych i łączymy prostą linią.
Przykład:
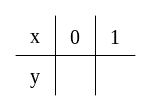
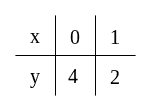

Liczba we wzorze, przy której nie stoi , to współczynnik , czyli wyraz wolny.
Przykład: Dla funkcji współczynnik jest równy .
Punkt to punkt przecięcia z osią .
Przykład: Dla funkcji punkt przecięcia z osią to .
Jeśli funkcja jest postaci , to . Taka funkcja przechodzi przez początek układu współrzędnych.
Przykład: Dla funkcji współczynnik wynosi .
Liczba we wzorze, przy której stoi , to współczynnik , czyli współczynnik kierunkowy.
Przykład: Dla funkcji współczynnik wynosi .
Współczynnik mówi nam, jaka jest monotoniczność funkcji.
Jeśli , to funkcja jest rosnąca.
Jeśli , to funkcja jest malejąca.
Przykład: Funkcja jest malejąca, ponieważ .
Jeśli funkcja jest postaci , to jest to funkcja stała. W takim wypadku .
Przykład: Funkcja jest stała. Współczynnik kierunkowy dla tej funkcji jest równy zero.
Miejsce zerowe to taka wartość -a, dla której wartość -a wynosi zero. Dla funkcji liniowej możemy wyznaczyć je ze wzoru
Przykład: Dla funkcji miejsce zerowe to
Punkt przecięcia z osią to .
Przykład: Dla funkcji punkt przecięcia z osią to .
Własności funkcji liniowej - przykładowe zadania maturalne
Rozwiązywanie równań liniowych
Dzięki tobie zrozumiałem funkcje liniowe <3
Ale super! <3 Dzięki za komentarz 🙂
Cześć. Jakiego programu używasz do generowania takich ładnych wykresów funkcji? 🙂
sequi maxime nobis cum aut quae et quod blanditiis earum similique nesciunt. reprehenderit expedita ut est omnis consequatur ea eveniet sed a suscipit placeat illum nobis et et modi.
repellat earum qui ad et aut expedita non. perferendis sunt quas veritatis reiciendis dolor aperiam quis et delectus.
dolorum culpa ut hic sunt aut vel saepe repellat non. aliquam reiciendis repellendus reiciendis omnis ad qui ex totam distinctio. quam laboriosam quia eius esse voluptatem eaque eligendi quod ab. dolorem est accusantium non tenetur praesentium ratione sit quia quod numquam maxime consequatur qui. voluptatem aspernatur quis consequatur repudiandae aut nihil.