Spis treści
- Wzór na prawdopodobieństwo
- Obliczanie prawdopodobieństwa
- Reguła dodawania
Wzór na prawdopodobieństwo
Powiedzmy, że chcemy obliczyć, z jakim prawdopodobieństwem podczas rzutu kostką wypadnie liczba . Aby to zrobić, korzystamy z poniższego wzoru:
oznacza liczbę wszystkich zdarzeń elementarnych. Co to są te zdarzenia elementarne? Są to wszystkie możliwe zdarzenia, które mogą zajść w rozważanej sytuacji. U nas rozważaną sytuacją jest rzut kostką, a zdarzeniem elementarnym będzie wylosowanie liczby (jakiejkolwiek) podczas rzutu kostką. Pól na kostce mamy , zatem na sposobów możemy wylosować liczbę. Stąd .
oznacza liczbę sposobów, na które może zajść zdarzenie, którego prawdopodobieństwo liczymy. My wyznaczamy prawdopodobieństwo, że podczas rzutu kostką wypadnie liczba , czyli u nas oznacza liczbę sposobów, na które możemy wylosować liczbę . Na kostce mamy jedno pole z liczbą , zatem .
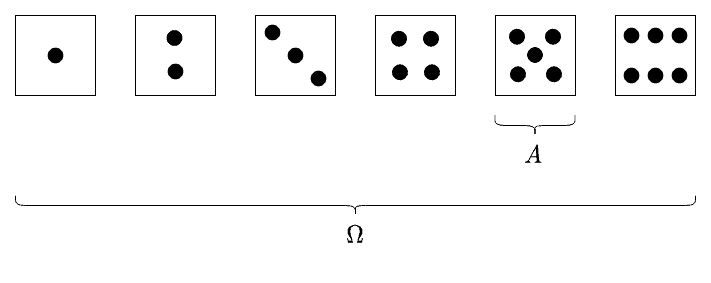
Stąd prawdopodobieństwo, że podczas rzutu kostką wypadnie liczba , wynosi
A teraz policzmy prawdopodobieństwo, że podczas rzutu kostką otrzymamy liczbę większą niż .
, czyli liczba sposobów na wyrzucenie jakiejkolwiek liczby oczek, pozostaje taka sama: .
Teraz |A|, czyli liczba sposobów na wyrzucenie liczby większej niż . Na kostce mamy dwa pola z liczbą większą niż , stąd .

Możemy obliczyć prawdopodobieństwo:
Dobry zwyczaj mówi, by wynik przedstawiać w postaci nieskracalnego ułamka, więc skrócimy go sobie przez .
Po obliczeniu prawdopodobieństwa zawsze zwróć uwagę, czy jest to liczba od do . Jeśli wyszło Ci ujemne albo większe od , to na pewno gdzieś jest błąd.
Jak widzisz, sama idea nie jest jakoś szczególnie skomplikowana, problemy pojawiają się natomiast przy ustalaniu, ile jest sposobów na wylosowanie czegoś. W dalszej części możesz zobaczyć, jak to działa w trochę trudniejszych przypadkach 🙂
Obliczanie prawdopodobieństwa
Chcemy obliczyć prawdopodobieństwo, że wylosujemy czerwoną kulkę. Oznaczymy sobie to zdarzenie wielką literą .
Teraz chcemy obliczyć prawdopodobieństwo tego zdarzenia, czyli .
, to liczba sposobów, na które możemy wylosować jakąkolwiek kulkę.
Teraz , czyli liczba sposobów na wylosowanie czerwonej kulki. W pudełku mamy czerwonych kulek, stąd .
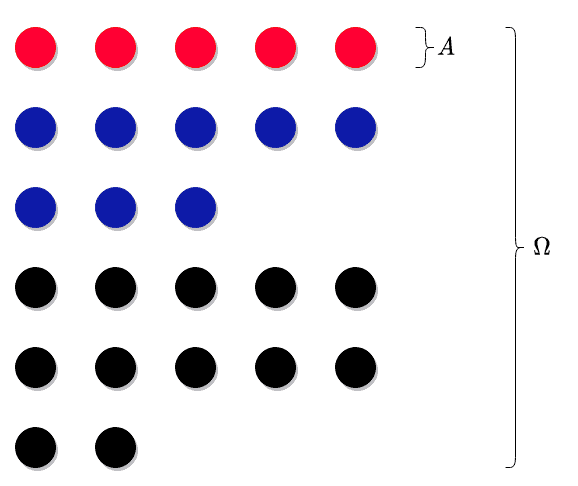
Teraz obliczamy prawdopodobieństwo wylosowania czerwonej kulki:
Prawdopodobieństwo przedstawiamy w formie nieskracalnego ułamka:
Odpowiedź: Prawdopodobieństwo wylosowania czerwonej kulki wynosi .
Pokażę Ci teraz na innym przykładzie, jak to działa, gdy zdarzenie oznaczymy inaczej niż .
Najpierw określamy zdarzenie, którego prawdopodobieństwo chcemy policzyć. U nas tym zdarzeniem jest wylosowanie liczby podzielnej przez . Tym razem oznaczymy je jako .
Teraz wyznaczamy oraz .
to liczba sposobów, na które możemy wylosować dowolną liczbę z zadanego przedziału. W przedziale od do jest liczb, dlatego dowolną liczbę możemy wylosować na sposobów. Stąd .
to liczba sposobów, na ktore możemy wylosować liczbę podzielną przez . Wypiszmy sobie te liczby:
Liczb podzielnych przez mamy , możemy więc taką liczbę wylosować na sposobów. Stąd .
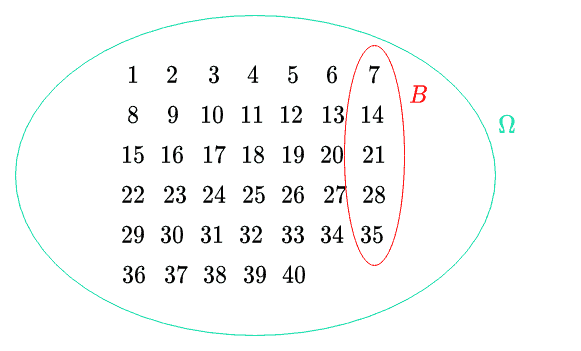
Chcę zwrócić Twoją uwagę na różnicę między i .
to zbiór, który zawiera w sobie jakieś elementy. Na przykład u nas . Natomiast to moc zbioru , czyli liczba elementów w zbiorze. U nas .
Teraz możemy obliczyć prawdopodobieństwo, czyli :
Odpowiedź: Prawdopodobieństwo wylosowania liczby podzielnej przez wynosi .
Reguła dodawania
Reguła dodawania to takie coś, co każdy stosuje, nawet nie wiedząc, że ona istnieje. Pokażę Ci od razu na przykładzie, na czym to polega.
Robiliśmy bardzo podobne zadanie - wtedy chcieliśmy wylosować czerwoną kulkę, teraz interesuje nas kulka czerwona lub niebieska. I teraz tak: kulkę czerwoną możemy wylosować na pięć sposobów, natomiast kulkę niebieską na osiem sposobów. Reguła dodawania mówi, że kulkę czerwoną lub niebieską możemy wylosować na sposobów. Warunek jest taki, że zbiory nie mogą mieć elementów wspólnych - i tu faktycznie nie mają, bo nie ma kulki, która byłaby i niebieska, i czerwona. Dlatego .
Natomiast , bo na tyle sposobów możemy wylosować jakąkolwiek kulkę.
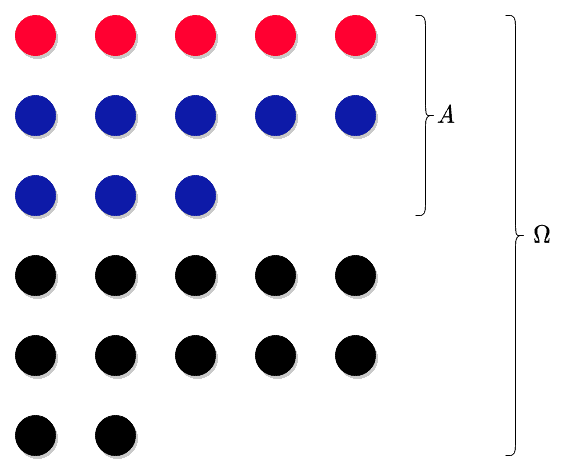
Obliczamy prawdopodobieństwo.
Odpowiedź: Prawdopodobieństwo, że wylosujemy kulkę czerwoną lub niebieską, jest równe .
Jak wspomniałam, przy tego typu zadaniach musimy pilnować, czy zbiory, które sumujemy, nie mają elementów wspólnych. A co zrobić, jeśli mają?
Mamy grupę dwudziestu czterech osób, więc losowo możemy wybrać jedną osobę na sposoby. Stąd . Teraz . Rozpiszmy sobie, co wiemy z zadania.
kręgle: osób
piłka nożna: osób
ani jedno, ani drugie: osób
Jeśli się przyjrzysz to zobaczysz, że podane wyżej liczby nie sumują nam się do dwudziestu czterech: .

Skąd te dwie nadmiarowe osoby? Stąd, że dwie osoby grają i w kręgle, i w piłkę nożną.

Jeśli więc po prostu dodamy osoby grające w kręgle i w piłkę nożną, to te dwie osoby policzymy dwa razy. W takiej sytuacji musimy od naszej sumy odjąć część wspólną.
kręgle: osób
piłka nożna: osób
piłka nożna i kręgle: osoby
piłka nożna lub kręgle:
Stąd . Teraz liczymy prawdopodobieństwo.
Odpowiedź: Prawdopodobieństwo wylosowania osoby grającej w kręgle lub w piłkę nożną jest równe .
Pokażę Ci teraz trzy bardzo podobne zadania, w których będziemy wyznaczać inaczej właśnie ze względu na tę nieszczęsną część wspólną.
Najpierw , czyli liczba sposobów, na które możemy wylosować jakąkolwiek liczbę. Liczb mamy , więc .
Teraz , czyli liczba sposobów, na które możemy wylosować liczbę podzielną przez lub . Wypiszmy sobie te liczby.
liczby podzielnych przez : - trzy liczby
liczby podzielne przez : - dwie liczby
W tych dwóch zbiorach nie mamy części wspólnej - nie ma tu liczby, która byłaby podzielna i przez , i przez , dlatego stosujemy regułę dodawania.
.
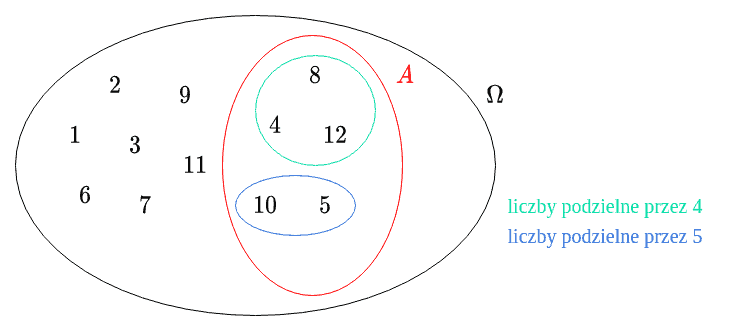
Teraz możemy obliczyć prawdopodobieństwo.
Odpowiedź: Prawdopodobieństwo wylosowania liczby podzielnej przez lub wynosi .
Teraz drugie zadanie.
, czyli liczba sposobów, na które możemy wylosować jakąkolwiek liczbę, pozostaje taka sama: .
Teraz . Wypiszmy sobie liczby podzielne przez oraz przez .
liczby podzielne przez : - cztery liczby
liczby podzielne przez : - trzy liczby
Gdybyśmy teraz zastosowali regułę dodawania, to wyszłoby nam, że , ale tak nie jest. Reguła dodawania zakłada, że zbiory, które uwzględniamy, nie mają wspólnych elementów, a u nas liczba jest podzielna i przez , i przez , więc stosując regułę dodawania policzylibyśmy ją dwa razy.
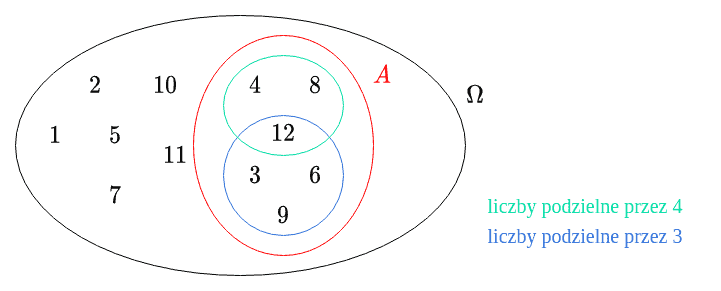
W takiej sytuacji musimy od sumy odjąć część wspólną.
liczby podzielne przez : - cztery liczby
liczby podzielne przez : - trzy liczby
liczby podzielne przez i : - jedna liczba
Teraz możemy obliczyć prawdopodobieństwo.
Odpowiedź: Prawdopodobieństwo wylosowania liczby podzielnej przez lub jest równe .
Trzeci przykład będzie nieco inny.
Tak jak poprzednio mamy liczb, więc .
Teraz . Tutaj też mamy dwa warunki, ale zwróć uwagę, że nie mamy słowa lub, tylko i - to znaczy, że mamy znaleźć liczby, które są podzielne i przez , i przez . Takie liczby mamy dwie: oraz - stąd .
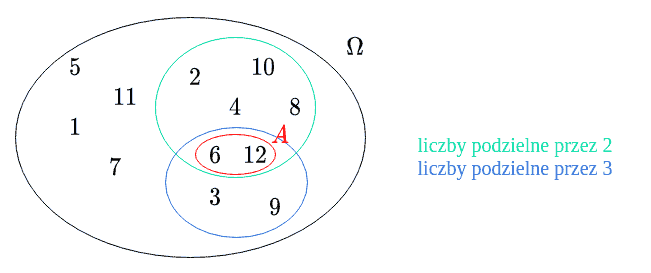
Teraz obliczymy prawdopodobieństwo.
Odpowiedź: Prawdopodobieństwo wylosowania liczby podzielnej przez i jest równe .
Prawdopodobieństwo obliczamy ze wzoru
W tym wzorze |A|, to liczba sposobów, na które może zajść zdarzenie, którego prawdopodobieństwo liczymy, natomiast oznacza liczbę zdarzeń elementarnych, czyli wszystkich możliwych zdarzeń, które mogą zajść w rozważanej sytuacji.
Przykład: Jeśli mamy obliczyć prawdopodobieństwo, że podczas rzutu kostką wypadnie parzysta liczba, to , ponieważ na kostce mamy trzy pola z parzystą liczbą (, oraz ), natomiast , ponieważ mamy sześć pól na kostce, które mogą wypaść. Wtedy prawdopodobieństwo wynosi
Podczas wyznaczania oraz uwzględniamy opcje, które się powtarzają.
Przykład: Jeśli mamy w pudełku trzy kulki niebieskie i pięć czerwonych, to jakąkolwiek kulkę możemy wylosować na osiem sposobów (nie na dwa).
Jeśli przykład jest bardziej skomplikowany, możemy wypisać sobie wszystkie możliwości.
Przykład: Jeśli mamy obliczyć prawdopobieństwo, że podczas losowania jednej liczby spośród wszystkich liczb dwucyfrowych otrzymamy liczbę, która jest podzielna przez , to możemy wypisać sobie wszystkie takie liczby.
Mamy osiem takich liczb, stąd .
We wzorze na prawdopodobieństwo mamy literę , natomiast może to być dowolna litera alfabetu i zawsze będzie oznaczała zdarzenie, którego prawdopodobieństwo liczymy.
Przykład: Jeśli zdarzenie oznaczymy jako , to wzór na prawdopodobieństwo będzie wyglądał następująco:
Jeśli zdarzenie może zajść na sposobów, a zdarzenie może zajść na sposobów, to zdarzenie lub może zajść na sposobów, o ile te zdarzenia się wzajemnie wykluczają. Nazywamy to regułą dodawania.
Przykład: Jeśli kulkę czerwoną możemy wylosować na pięć sposobów, a kulkę niebieską możemy wylosować na siedem sposobów, to kulkę czerwoną lub niebieską możemy wylosować na sposobów (stosujemy regułę dodawania, bo są to zdarzenia wykluczające się - nie można wylosować kulki, która będzie jednocześnie czerwona i niebieska).
Jeśli zdarzenia się nie wykluczają, to od sumy musimy odjąć część wspólną.
Przykład: Jeśli pięć osób gra na flecie, a cztery osoby grają na skrzypcach, przy czym dwie osoby grają na obu instrumentach, to osobę, która gra na flecie lub skrzypcach możemy wylosować na sposobów.
Prawdopodobieństwo jest zawsze liczbą od do , lub, jeśli podajemy je w procentach, od do . Jeśli prawdopodobieństwo jest równe , to nie ma możliwości, by zaszło dane zdarzenie.
Przykład: Prawdopodobieństwo, że podczas rzutu kostką wylosujemy liczbę , jest równe .
Natomiast jeśli prawdopodobieństwo jest równe , to znaczy, że zdarzenie na pewno wystąpi.
Przykład: Prawdopodobieństwo, że podczas rzutu kostką wylosujemy liczbę mniejszą niż , jest równe .