Spis treści
- Co to jest logarytm?
- Jak obliczyć logarytm?
- Jak obliczać logarytmy z ułamkami?
- Jak obliczać logarytmy z pierwiastkami?
- Co zrobić, gdy logarytm nie ma podstawy?
- Kiedy logarytm jest równy zero?
- Kiedy logarytm jest równy jeden?
Co to jest logarytm?
Definicja logarytmu wygląda tak:
W tym wyrażeniu , oraz są liczbami. Zazwyczaj znamy liczby i , a musimy znaleźć liczbę (czyli obliczyć logarytm).
W gruncie rzeczy logarytm to po prostu odwrotność potęgowania. Spójrz na przykłady:
- , ponieważ ;
- , ponieważ ;
- , ponieważ .
- Zapis czytamy "logarytm przy podstawie z liczby ".
- Liczbę nazywamy podstawą logarytmu.
- Liczbę nazywamy liczbą logarytmowaną.
- Obie te liczby muszą być dodatnie, a dodatkowo liczba nie może być równa .
- Jeśli chodzi o liczbę , czyli wynik logarytmu, to nie mamy żadnych ograniczeń.
- jeśli nie mamy wykładnika, to jest on równy ;
np. - jeśli mamy ułamek, to możemy go odwrócić przy pomocy ujemnej potęgi;
np. - jeśli mamy pierwiastek, to możemy się go pozbyć przy pomocy ułamkowej potęgi.
np.
Być może zastanawiasz się, po co w takim razie komplikować sobie życie logarytmami, skoro mamy potęgi. Okazuje się, że logarytmy, choć przy pierwszym kontakcie mogą przyprawić o atak paniki, bardzo ułatwiają wiele operacji matematycznych, co przydaje się na przykład przy opisie różnych zjawisk przyrodniczych.
Zanim przejdziemy dalej, trochę formalności.
No dobra, to teraz razem przebrniemy przez to wszystko krok po kroku 🙂
Jak obliczyć logarytm?
Aby obliczyć wartość logarytmu, skorzystamy z jego definicji:
Będziemy zamieniać logarytm na potęgowanie, bo z tym łatwiej sobie poradzić. W związku z tym, że w tym wpisie często będą pojawiać się nazwy związane z potęgami, a sporo osób je myli, na początku upewnijmy się, że gdy mówimy "potęga", to oboje mamy na myśli to samo:
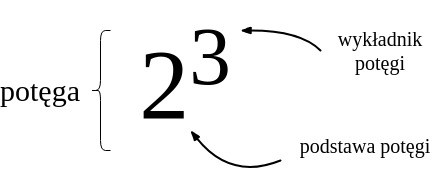
Zaczniemy od takiego zadania:
Nie znamy wyniku tego logarytmu, więc oznaczymy go jako .
Porównujmy to do lewej części naszego wzoru.
U nas , i . Podstawiamy to teraz do prawej części wzoru:
Następny krok, to takie przekształcenie tego wyrażenia, by po obu stronach pojawiły się potęgi o takiej samej podstawie. W naszym przypadku możemy zapisać jako . Wstawiamy to do naszego równania.
Skoro mamy takie same podstawy, to i wykładniki muszą być takie same. Mamy tu zapis " do jakiejś nieznanej potęgi równa się do trzeciej potęgi". Stąd wiemy, że ta "jakaś potęga" musi być równa :
Jak może pamiętasz, na samym początku zadania przez oznaczyliśmy wynik naszego logarytmu:
Ponieważ obliczyliśmy , możemy go teraz wstawić, tym samym podając wynik logarytmu:
Przećwiczmy to na jeszcze jednym przykładzie.
Najpierw oznaczmy sobie wynik logarytmu przez :
Porównajmy sobie nasz logarytm do wzoru:
Tutaj . Podstawiamy to do prawej części wzoru:
Teraz chcemy po obu stronach otrzymać potęgi o takiej samej podstawie. Zamienimy więc na :
Podstawy są takie same, więc możemy przyrównać do siebie wykładniki:
Ponieważ to wynik naszego logarytmu, to
Teraz trochę trudniejszy przykład, choć będzie wyglądał bardzo podobnie.
Najpierw, jak zawsze, oznaczę wynik tego logarytmu jako .
Porównajmy to ze wzorem i zamieńmy na potęgowanie.
Chcę otrzymać po obu stronach potęgi o takiej samej podstawie. Tym razem łatwiej będzie mi przekształcić lewą stronę, a nie, jak do tej pory, prawą. Zamienię na :
Po lewej stronie nie mamy jeszcze jednej potęgi. Aby ją otrzymać, wykonamy potęgowanie potęgi (możesz o tym poczytać tutaj).
Na tym etapie powinniśmy porównać wykładniki. Problem polega na tym, że po prawej stronie nie mamy wykładnika. Możemy to jednak łatwo naprawić - wystarczy, że zapiszemy jako .
Teraz mogę już przyrównać do siebie wykładniki:
Aby wyznaczyć , wykonuję obustronne dzielenie przez (o rozwiązywaniu równań możesz poczytać tutaj).
Ponieważ oznaczyliśmy sobie jako , to otrzymujemy następujący wynik:
Czasami może być tak, że obie strony wymagają przekształcenia. Tak będzie w tym przykładzie:
Początek jest zawsze taki sam - oznaczamy wynik logarytmu jako i zamieniamy logarytm na potęgowanie.
Teraz chcemy mieć po obu stronach równania potęgi o takiej samej podstawie. Problem polega na tym, że ósemki nie da się zapisać jako cztery do jakiejś potęgi (to znaczy da się, ale będzie to bardzo brzydka potęga). Możemy natomiast obie liczby zapisać jako potęgę dwójki: to , a to . Wstawiam to do naszego równania.
Aby mieć po obu stronach jedną potęgę, wykonuję potęgowanie potęgi po lewej stronie.
Mamy już potęgi o takiej samej podstawie, możemy więc przyrównać do siebie wykładniki.
Aby otrzymać , dzielę obustronnie przez :
Na początku zapisaliśmy, że , dlatego
Jak obliczać logarytmy z ułamkami?
Do tej pory w logarytmach pojawiały nam się same liczby naturalne. Teraz zobaczmy, co się stanie, jeśli pojawią się ułamki.
Najpierw, jak zawsze, oznaczamy wynik logarytmu jako .
Następnie zamieniamy logarytm na potęgowanie:
Teraz chcemy, żeby po obu stronach były potęgi o takich samych podstawach. U mnie tą podstawą będzie . Aby z zrobić , skorzystam z tego, że jeśli podniesiemy liczbę do ujemnej potęgi, to zostaje ona "odwrócona do góry nogami" (pisałam o tym w tym poście) .
Teraz, gdy mamy takie same podstawy, mogę przyrównać wykładniki:
A ponieważ przez oznaczyliśmy sobie , to
Teraz nieco trudniejszy przykład:
Początek taki sam jak zawsze 😉
Teraz sprowadzamy sobie potęgi do tej samej podstawy. U mnie będzie to . Najpierw zamienię prawą stronę: to .
Teraz lewa strona. Skorzystam w tego samego wzoru, co ostatnio:
Wykonuję potęgowanie potęgi:
Mamy takie same podstawy, możemy przyrównać do siebie wykładniki:
Aby otrzymać , mnożę obustronnie przez :
Stąd
Jak obliczać logarytmy z pierwiastkami?
Sprawa jest chyba najbardziej skomplikowana, gdy w logarytmie występują pierwiastki, ale to też ogarniemy 🙂
Początek zawsze taki sam:
Teraz chcemy uzyskać po obu stronach potęgi o takiej samej podstawie. Aby to zrobić, zamienię pierwiastek na potęgę. Skorzystamy z tego wzoru:
O zamienianiu pierwiastka na potęgę pisałam tutaj .
Mamy takie same podstawy, przyrównujemy wykładniki:
Stąd
Teraz trudniejszy przykład:
Oznaczamy logarytm jako .
Zamieniamy logarytm na potęgowanie:
Teraz sprowadzamy obie strony do takiej samej podstawy. U mnie będzie to . Przy pomocy tego samego wzoru, co poprzednio, zamienimy na potęgę.
Nie mamy nad dzióbkiem pierwiastka żadnej liczby - to znaczy, że domyślnie jest to .
Po prawej stronie mamy mnożenie potęg (a raczej będziemy mieć, gdy zapiszemy jako ), więc wykładniki się dodają (o działaniach na potęgach możesz poczytać tutaj).
Aby wykonać dodawanie, potrzebujemy wspólnego mianownika.
Mamy już takie same podstawy, więc możemy przyrównać wykładniki:
Otrzymaliśmy wynik logarytmu:
Co zrobić, gdy logarytm nie ma podstawy?
Pokażę Ci to na przykładzie.
Na początku oznaczamy wynik logarytmu jako :
Teraz robimy jeden dodatkowy krok - dopisujemy w podstawie.
A dalej robimy wszystko dokładnie tak samo, jak zwykle - zamieniamy logarytm na potęgowanie, sprowadzamy do takiej samej podstawy i przyrównujemy wykładniki.
Kiedy logarytm jest równy zero?
Zostały nam do omówienia dwa szczególne przypadki logarytmów. Pierwszy z nich to taki logarytm, w którym liczba logarytmowana wynosi , na przykład taki:
Oznaczamy wynik logarytmu jako i zamieniamy na potęgowanie:
Teraz przychodzi ten moment, gdy chcemy otrzymać po obu stronach potęgi o tej samej podstawie. Na pierwszy rzut oka sprawa wydaje się skomplikowana, ale w rzeczywistości musimy jedynie pamiętać, że dowolna liczba podniesiona do zerowej potęgi daje nam .
Skorzystamy z tego i przedstawimy jako .
Przyrównujemy wykładniki:
Ten przykład doprowadził nas do następującego wzoru:
Innymi słowy - jeśli liczba logarytmowana jest równa , to logarytm zawsze będzie równy , niezależnie od podstawy.
Kiedy logarytm jest równy jeden?
Ostatni przykład na dziś:
Jak zawsze - wynik logarytmu oznaczamy jako i zamieniamy na potęgowanie.
Po obu stronach chcemy mieć takie same podstawy - i w zasadzie już mamy. Tylko żeby przyrównać do siebie wykładniki, musimy najpierw mieć te wykładniki, dlatego zapiszę jako .
No to przyrównujemy wykładniki i podajemy wynik.
Ten przykład pokazał nam, że jeśli podstawa logarytmu i liczba logarytmowana są takie same, to taki logarytm zawsze będzie równy .
I na koniec: czasem trafia nam się sytuacja, w której na rzęsach stajemy, a logarytmu nie da się policzyć. No nie da się (tak naprawdę się da, tylko wynik jest brzydki). Opcje mamy dwie: albo coś robimy źle, albo tego logarytmu nie trzeba wcale liczyć - tak jest często wtedy, gdy mamy działania na logarytmach. Opisałam je w tym wpisie.
Definicja logarytmu:
- podstawa logarytmu, ,
- liczba logarytmowana,
Zapis czytamy "logarytm przy podstawie z liczby ".
Aby obliczyć logarytm:
1) oznaczamy sobie jego wynik jako ;
np.
2) zamieniamy go na potęgowanie;
np.
3) sprowadzamy potęgi do takiej samej podstawy;
np.
4) przyrównujemy wykładniki;
np.
Na trzecim etapie możemy napotkać kilka problemów:
Jeśli logarytm nie ma podstawy, to możemy dopisać podstawę . Taki logarytm nazywamy logarytmem dziesiętnym.
np.
Szczególne przypadki logarytmów:
np.
np.
Działania na logarytmach
Działania na potęgach - część 1
Potęgi o ujemnym wykładniku
Potęgi o ułamkowym wykładniku
świetny materiał, bardzo dobrze wytłumaczone, dziękuję !
Cieszę się, że mogłam pomóc 🙂
Ten wykład o logarytmach rozjaśnił mi w głowie. Tak powinni uczyć nauczyciele w szkołach.
Ojej, dziękuję! 🙂
Super tlumaczenie mam 67 lat i musze udzielic pomocy mojemu wnukowi . Musialem przypomniec sobie zasady ito mi bardzo pomoglo . Dzieki .
Bardzo się cieszę! 🙂