Spis treści
- Mnożenie i dzielenie potęg - wzory i przykłady
- Potęgowanie potęgi - wzór i przykłady
- Przykładowe zadania z wykorzystaniem działań na potęgach
Na początku przypomnijmy sobie trzy pojęcia, których będę używać w tym wpisie bardzo często:
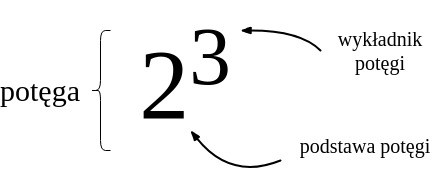
A teraz przechodzimy do części właściwej 🙂
Mnożenie i dzielenie potęg
Mnożyć i dzielić potęgi możemy w dwóch sytuacjach - gdy mamy takie same podstawy lub takie same wykładniki.
Takie same podstawy
Gdy mnożymy dwie potęgi i mają one takie same podstawy, to wykładniki tych potęg się dodają.
Przykłady:
Natomiast gdy dzielimy dwie potęgi o takich samych podstawach, to ich wykładniki się odejmują.
Przykłady:
Dzielenie możemy zapisać także w postaci ułamka:
Przykład:
Mnożenie i dzielenie potęg możemy też łączyć w jednym przykładzie:
Takie same wykładniki
Gdy mamy różne podstawy, ale takie same wykładniki, to możemy sobie "skleić" dwie potęgi w jedną. Przy mnożeniu potęg wygląda to tak:
Przykłady:
Natomiast przy dzieleniu tak:
Przykłady:
Tak jak poprzednio, dzielenie możemy przedstawić w formie ułamka:
Przykład:
Tak jak poprzednio, tu również mnożenie i dzielenie potęg możemy łączyć w jednym przykładzie:
Potęgowanie potęgi
Gdy chcemy jakąś potęgę podnieść do potęgi jeszcze raz, korzystamy z tego wzoru:
Przykład:
- - tu mamy nawiasy, więc stosujemy wzór;
- - tu nie mamy nawiasów, więc do trzeciej potęgi podnosimy samą dwójkę.
Przykładowe zadania z wykorzystaniem działań na potęgach
Najczęściej spotykamy się z trzema typami zadań: "oblicz", "doprowadź do najprostszej postaci" oraz "zapisz w postaci jednej potęgi" (może być też napisane, jakiej konkretnie, np. "zapisz w postaci potęgi liczby "). Natomiast generalnie zasada jest taka, że jeśli pojawiają się potęgi, które są duże i ich liczenie jest bez sensu, to trzeba skorzystać ze wzorów na działania na potęgach, nawet jeśli początkowo żaden wzór nam nie pasuje. No ale po kolei 🙂
Oblicz:
Możemy zauważyć, że na górze mamy takie same wykładniki. Skorzystamy najpierw z tego wzoru:
Powstały nam takie same podstawy, możemy więc skorzystać z tego wzoru.
No a to po prostu 🙂
Oblicz:
Tutaj mamy takie same podstawy. Zacznę od działań w nawiasach, a że są dwie pary nawiasów, to wybieramy te najbardziej w środku. Korzystamy ze wzoru na mnożenie potęg.
Teraz korzystamy ze wzoru na potęgowanie potęgi.
Udało nam się pozbyć jednego nawiasu, teraz wykonujemy działania wewnątrz drugiego. Korzystamy ze wzoru na dzielenie potęg.
Znowu mamy potęgowanie potęgi.
No a to już możemy łatwo obliczyć 🙂
Doprowadź do najprostszej postaci:
Tu w podstawie zamiast liczby mamy , ale zasady są dokładnie te same 🙂 Tą dwójką, którą mamy z przodu, możemy się póki co zupełnie nie przejmować, skupiamy się na działaniach na -ach (możemy tak zrobić, bo mnożenie jest przemienne, więc równie dobrze moglibyśmy tę dwójkę postawić na końcu ułamka). Zaczynamy od nawiasów.
Teraz zajmę się wyrażeniem . Nie mamy nawiasów, więc nie stosujemy wzoru, tylko po prostu podnosimy trójkę do drugiej potęgi.
Teraz możemy się zająć mnożeniem i dzieleniem potęg. Najpierw góra.
Teraz dół. Zapiszemy sobie jako , bo potrzebujemy mieć wykładnik, żeby wykonać działania na potęgach.
Zostało nam ostatnie działanie do wykonania. Tu trzeba bardzo uważać, żeby nam się nie pomyliło z minusami.
To jest najprostsza postać 🙂
Zapisz w postaci jednej potęgi:
Jak widzisz, nie mamy ani takich samych podstaw, ani wykładników. Możemy jednak zauważyć, że wszystkie podstawy da się zapisać jako do jakiejś potęgi: to , to , a to .
Udało nam się uzyskać takie same podstawy, więc teraz wykonujemy działania na potęgach. Na górze mamy mnożenie potęg.
Teraz zajmiemy się dołem. Zaczniemy od pozbycia się nawiasów, a więc wykonamy potęgowanie potęgi.
Porządkujemy dalej dół, wykonując dzielenie potęg.
Zostało nam już tylko pozbycie się ułamka.
No i mamy 🙂
Na koniec zadanie maturalne, które bardzo fajnie pokazuje, jak działania na potęgach potrafią ułatwić życie.
Liczba naturalna w zapisie dziesiętnym ma
A. cyfr B. cyfr C. cyfr D. cyfr
No więc po pierwsze: nie liczymy tego! Próbujemy jakoś tak pokombinować, żeby otrzymać albo takie same podstawy, albo takie same wykładniki. Na takie same podstawy mamy niewielkie szanse, natomiast na takie same wykładniki jak najbardziej:
Skorzystaliśmy tutaj z tego wzoru:
Pozwolił on nam zapisać jako . Teraz użyjemy tego wzoru:
Przekształcamy dalej:
I teraz tak: to , czyli jeden i zer. Gdy pomnożymy to przez , otrzymamy , czyli pięć i zer - tak więc liczba ma cyfr.
Odpowiedź B.
Generalnie zasada w tego typu zadaniach jest prosta: patrzymy na wzory i szukamy takiego, który pasuje. Jeśli żaden nie pasuje, to zastanawiamy się, do którego jest najbliżej i staramy się jakoś tak pokombinować, żeby doprowadzić do postaci, którą mamy we wzorze.
W kontekście działań na potęgach posługujemy się trzema kluczowymi pojęciami:

Możemy mnożyć i dzielić potęgi, gdy mamy takie same podstawy lub takie same wykładniki.
Gdy mamy takie same podstawy, mnożenie i dzielenie potęg wygląda tak:
Przykład:
Przykład:
Przykład:
Gdy mamy takie same wykładniki, wzory na mnożenie i dzielenie potęg wyglądają tak:
Przykład:
Przykład:
Przykład:
Kolejnym działaniem jest potęgowanie potęgi:
Przykład:
Gdy nie mamy nawiasów, potęgujemy sam wykładnik.
Przykład:
Działania na potęgach - część 2
Potęgi o ujemnym wykładniku
Potęgi o ułamkowym wykładniku
magqai
vz58u9
spoko
VPS SERVER
Высокоскоростной доступ в Интернет: до 1000 Мбит/с
Скорость подключения к Интернету — еще один важный фактор для успеха вашего проекта. Наши VPS/VDS-серверы, адаптированные как под Windows, так и под Linux, обеспечивают доступ в Интернет со скоростью до 1000 Мбит/с, что гарантирует быструю загрузку веб-страниц и высокую производительность онлайн-приложений на обеих операционных системах.
win79
オンラインカジノとオンラインギャンブルの現代的展開
オンラインカジノの世界は、技術の進歩と共に急速に進化しています。これらのプラットフォームは、従来の実際のカジノの体験をデジタル空間に移し、プレイヤーに新しい形式の娯楽を提供しています。オンラインカジノは、スロットマシン、ポーカー、ブラックジャック、ルーレットなど、さまざまなゲームを提供しており、実際のカジノの興奮を維持しながら、アクセスの容易さと利便性を提供します。
一方で、オンラインギャンブルは、より広範な概念であり、スポーツベッティング、宝くじ、バーチャルスポーツ、そしてオンラインカジノゲームまでを含んでいます。インターネットとモバイルテクノロジーの普及により、オンラインギャンブルは世界中で大きな人気を博しています。オンラインプラットフォームは、伝統的な賭博施設に比べて、より多様なゲーム選択、便利なアクセス、そしてしばしば魅力的なボーナスやプロモーションを提供しています。
安全性と規制
オンラインカジノとオンラインギャンブルの世界では、安全性と規制が非常に重要です。多くの国々では、オンラインギャンブルを規制する法律があり、安全なプレイ環境を確保するためのライセンスシステムを設けています。これにより、不正行為や詐欺からプレイヤーを守るとともに、責任ある賭博の促進が図られています。
技術の進歩
最新のテクノロジーは、オンラインカジノとオンラインギャンブルの体験を一層豊かにしています。例えば、仮想現実(VR)技術の使用は、プレイヤーに没入型のギャンブル体験を提供し、実際のカジノにいるかのような感覚を生み出しています。また、ブロックチェーン技術の導入は、より透明で安全な取引を可能にし、プレイヤーの信頼を高めています。
未来への展望
オンラインカジノとオンラインギャンブルは、今後も技術の進歩とともに進化し続けるでしょう。人工知能(AI)の更なる統合、モバイル技術の発展、さらには新しいゲームの創造により、この分野は引き続き成長し、世界中のプレイヤーに新しい娯楽の形を提供し続けることでしょう。
この記事では、オンラインカジノとオンラインギャンブルの現状、安全性、技術の影響、そして将来の展望に焦点を当てています。この分野は、技術革新によって絶えず変化し続ける魅力的な領域です。
Tải Hit Club iOS
Tải Hit Club iOSHIT CLUBHit Club đã sáng tạo ra một giao diện game đẹp mắt và hoàn thiện, lấy cảm hứng từ các cổng casino trực tuyến chất lượng từ cổ điển đến hiện đại. Game mang lại sự cân bằng và sự kết hợp hài hòa giữa phong cách sống động của sòng bạc Las Vegas và phong cách chân thực. Tất cả các trò chơi đều được bố trí tinh tế và hấp dẫn với cách bố trí game khoa học và logic giúp cho người chơi có được trải nghiệm chơi game tốt nhất.
Hit Club – Cổng Game Đổi Thưởng
Trên trang chủ của Hit Club, người chơi dễ dàng tìm thấy các game bài, tính năng hỗ trợ và các thao tác để rút/nạp tiền cùng với cổng trò chuyện trực tiếp để được tư vấn. Giao diện game mang lại cho người chơi cảm giác chân thật và thoải mái nhất, giúp người chơi không bị mỏi mắt khi chơi trong thời gian dài.
Hướng Dẫn Tải Game Hit Club
Bạn có thể trải nghiệm Hit Club với 2 phiên bản: Hit Club APK cho thiết bị Android và Hit Club iOS cho thiết bị như iPhone, iPad.
Tải ứng dụng game:
Click nút tải ứng dụng game ở trên (phiên bản APK/Android hoặc iOS tùy theo thiết bị của bạn).
Chờ cho quá trình tải xuống hoàn tất.
Cài đặt ứng dụng:
Khi quá trình tải xuống hoàn tất, mở tệp APK hoặc iOS và cài đặt ứng dụng trên thiết bị của bạn.
Bắt đầu trải nghiệm:
Mở ứng dụng và bắt đầu trải nghiệm Hit Club.
Với Hit Club, bạn sẽ khám phá thế giới game đỉnh cao với giao diện đẹp mắt và trải nghiệm chơi game tuyệt vời. Hãy tải ngay để tham gia vào cuộc phiêu lưu casino độc đáo và đầy hứng khởi!
осоветуйте vps
Абузоустойчивый сервер для работы с Хрумером и GSA и различными скриптами!
Есть дополнительная системах скидок, читайте описание в разделе оплата
Виртуальные сервера VPS/VDS и Дедик Сервер: Оптимальное Решение для Вашего Проекта
В мире современных вычислений виртуальные сервера VPS/VDS и дедик сервера становятся ключевыми элементами успешного бизнеса и онлайн-проектов. Выбор оптимальной операционной системы и типа сервера являются решающими шагами в создании надежной и эффективной инфраструктуры. Наши VPS/VDS серверы Windows и Linux, доступные от 13 рублей, а также дедик серверы, предлагают целый ряд преимуществ, делая их неотъемлемыми инструментами для развития вашего проекта.
民意調查是什麼?民調什麼意思?
民意調查又稱為輿論調查或民意測驗,簡稱民調。一般而言,民調是一種為了解公眾對某些政治、社會問題與政策的意見和態度,由專業民調公司或媒體進行的調查方法。
目的在於通過網路、電話、或書面等媒介,對大量樣本的問卷調查抽樣,利用統計學的抽樣理論來推斷較為客觀,且能較為精確地推論社會輿論或民意動向的一種方法。
以下是民意調查的一些基本特點和重要性:
抽樣:由於不可能向每一個人詢問意見,所以調查者會選擇一個代表性的樣本進行調查。這樣本的大小和抽樣方法都會影響調查的準確性和可靠性。
問卷設計:為了確保獲得可靠的結果,問卷必須經過精心設計,問題要清晰、不帶偏見,且易於理解。
數據分析:收集到的數據將被分析以得出結論。這可能包括計算百分比、平均值、標準差等,以及更複雜的統計分析。
多種用途:民意調查可以用於各種目的,包括政策制定、選舉預測、市場研究、社會科學研究等。
限制:雖然民意調查是一個有價值的工具,但它也有其限制。例如,樣本可能不完全代表目標人群,或者問卷的設計可能導致偏見。
影響決策:民意調查的結果常常被政府、企業和其他組織用來影響其決策。
透明度和誠實:為了維護調查的可信度,調查組織應該提供其調查方法、樣本大小、抽樣方法和可能的誤差範圍等詳細資訊。
民調是怎麼調查的?
民意調查(輿論調查)的意義是指為瞭解大多數民眾的看法、意見、利益與需求,以科學、系統與公正的資料,蒐集可以代表全部群眾(母體)的部分群眾(抽樣),設計問卷題目後,以人工或電腦詢問部分民眾對特定議題的看法與評價,利用抽樣出來部分民眾的意見與看法,來推論目前全部民眾的意見與看法,藉以衡量社會與政治的狀態。
以下是進行民調調查的基本步驟:
定義目標和目的:首先,調查者需要明確調查的目的。是要了解公眾對某個政策的看法?還是要評估某個政治候選人的支持率?
設計問卷:根據調查目的,研究者會設計一份問卷。問卷應該包含清晰、不帶偏見的問題,並避免導向性的語言。
選擇樣本:因為通常不可能調查所有人,所以會選擇一部分人作為代表。這部分人被稱為“樣本”。最理想的情況是使用隨機抽樣,以確保每個人都有被選中的機會。
收集數據:有多種方法可以收集數據,如面對面訪問、電話訪問、郵件調查或在線調查。
數據分析:一旦數據被收集,研究者會使用統計工具和技術進行分析,得出結論或洞見。
報告結果:分析完數據後,研究者會編寫報告或發布結果。報告通常會提供調查方法、樣本大小、誤差範圍和主要發現。
解釋誤差範圍:多數民調報告都會提供誤差範圍,例如“±3%”。這表示實際的結果有可能在報告結果的3%範圍內上下浮動。
民調調查的質量和可信度很大程度上取決於其設計和實施的方法。若是由專業和無偏見的組織進行,且使用科學的方法,那麼民調結果往往較為可靠。但即使是最高質量的民調也會有一定的誤差,因此解讀時應保持批判性思考。
為什麼要做民調?
民調提供了一種系統性的方式來了解大眾的意見、態度和信念。進行民調的原因多種多樣,以下是一些主要的動機:
政策制定和評估:政府和政策制定者進行民調,以了解公眾對某一議題或政策的看法。這有助於制定或調整政策,以反映大眾的需求和意見。
選舉和政治活動:政黨和候選人通常使用民調來評估自己在選舉中的地位,了解哪些議題對選民最重要,以及如何調整策略以吸引更多支持。
市場研究:企業和組織進行民調以了解消費者對產品、服務或品牌的態度,從而制定或調整市場策略。
社會科學研究:學者和研究者使用民調來了解人們的社會、文化和心理特征,以及其與行為的關係。
公眾與媒體的期望:民調提供了一種方式,使公眾、政府和企業得以了解社會的整體趨勢和態度。媒體也經常報導民調結果,提供公眾對當前議題的見解。
提供反饋和評估:無論是企業還是政府,都可以透過民調了解其表現、服務或政策的效果,並根據反饋進行改進。
預測和趨勢分析:民調可以幫助預測某些趨勢或行為的未來發展,如選舉結果、市場需求等。
教育和提高公眾意識:通過進行和公布民調,可以促使公眾對某一議題或問題有更深入的了解和討論。
民調可信嗎?
民意調查的結果數據隨處可見,尤其是政治性民調結果幾乎可說是天天在新聞上放送,對總統的滿意度下降了多少百分比,然而大家又信多少?
在景美市場的訪問中,我們了解到民眾對民調有一些普遍的觀點。大多數受訪者表示,他們對民調的可信度存有疑慮,主要原因是他們擔心政府可能會在調查中進行操控,以符合特定政治目標。
受訪者還提到,民意調查的結果通常不會對他們的投票意願產生影響。換句話說,他們的選擇通常受到更多因素的影響,例如候選人的政策立場和政府做事的認真與否,而不是單純依賴民調結果。
從訪問中我們可以得出的結論是,大多數民眾對民調持謹慎態度,並認為它們對他們的投票決策影響有限。
民意調查是什麼?民調什麼意思?
民意調查又稱為輿論調查或民意測驗,簡稱民調。一般而言,民調是一種為了解公眾對某些政治、社會問題與政策的意見和態度,由專業民調公司或媒體進行的調查方法。
目的在於通過網路、電話、或書面等媒介,對大量樣本的問卷調查抽樣,利用統計學的抽樣理論來推斷較為客觀,且能較為精確地推論社會輿論或民意動向的一種方法。
以下是民意調查的一些基本特點和重要性:
抽樣:由於不可能向每一個人詢問意見,所以調查者會選擇一個代表性的樣本進行調查。這樣本的大小和抽樣方法都會影響調查的準確性和可靠性。
問卷設計:為了確保獲得可靠的結果,問卷必須經過精心設計,問題要清晰、不帶偏見,且易於理解。
數據分析:收集到的數據將被分析以得出結論。這可能包括計算百分比、平均值、標準差等,以及更複雜的統計分析。
多種用途:民意調查可以用於各種目的,包括政策制定、選舉預測、市場研究、社會科學研究等。
限制:雖然民意調查是一個有價值的工具,但它也有其限制。例如,樣本可能不完全代表目標人群,或者問卷的設計可能導致偏見。
影響決策:民意調查的結果常常被政府、企業和其他組織用來影響其決策。
透明度和誠實:為了維護調查的可信度,調查組織應該提供其調查方法、樣本大小、抽樣方法和可能的誤差範圍等詳細資訊。
民調是怎麼調查的?
民意調查(輿論調查)的意義是指為瞭解大多數民眾的看法、意見、利益與需求,以科學、系統與公正的資料,蒐集可以代表全部群眾(母體)的部分群眾(抽樣),設計問卷題目後,以人工或電腦詢問部分民眾對特定議題的看法與評價,利用抽樣出來部分民眾的意見與看法,來推論目前全部民眾的意見與看法,藉以衡量社會與政治的狀態。
以下是進行民調調查的基本步驟:
定義目標和目的:首先,調查者需要明確調查的目的。是要了解公眾對某個政策的看法?還是要評估某個政治候選人的支持率?
設計問卷:根據調查目的,研究者會設計一份問卷。問卷應該包含清晰、不帶偏見的問題,並避免導向性的語言。
選擇樣本:因為通常不可能調查所有人,所以會選擇一部分人作為代表。這部分人被稱為“樣本”。最理想的情況是使用隨機抽樣,以確保每個人都有被選中的機會。
收集數據:有多種方法可以收集數據,如面對面訪問、電話訪問、郵件調查或在線調查。
數據分析:一旦數據被收集,研究者會使用統計工具和技術進行分析,得出結論或洞見。
報告結果:分析完數據後,研究者會編寫報告或發布結果。報告通常會提供調查方法、樣本大小、誤差範圍和主要發現。
解釋誤差範圍:多數民調報告都會提供誤差範圍,例如“±3%”。這表示實際的結果有可能在報告結果的3%範圍內上下浮動。
民調調查的質量和可信度很大程度上取決於其設計和實施的方法。若是由專業和無偏見的組織進行,且使用科學的方法,那麼民調結果往往較為可靠。但即使是最高質量的民調也會有一定的誤差,因此解讀時應保持批判性思考。
為什麼要做民調?
民調提供了一種系統性的方式來了解大眾的意見、態度和信念。進行民調的原因多種多樣,以下是一些主要的動機:
政策制定和評估:政府和政策制定者進行民調,以了解公眾對某一議題或政策的看法。這有助於制定或調整政策,以反映大眾的需求和意見。
選舉和政治活動:政黨和候選人通常使用民調來評估自己在選舉中的地位,了解哪些議題對選民最重要,以及如何調整策略以吸引更多支持。
市場研究:企業和組織進行民調以了解消費者對產品、服務或品牌的態度,從而制定或調整市場策略。
社會科學研究:學者和研究者使用民調來了解人們的社會、文化和心理特征,以及其與行為的關係。
公眾與媒體的期望:民調提供了一種方式,使公眾、政府和企業得以了解社會的整體趨勢和態度。媒體也經常報導民調結果,提供公眾對當前議題的見解。
提供反饋和評估:無論是企業還是政府,都可以透過民調了解其表現、服務或政策的效果,並根據反饋進行改進。
預測和趨勢分析:民調可以幫助預測某些趨勢或行為的未來發展,如選舉結果、市場需求等。
教育和提高公眾意識:通過進行和公布民調,可以促使公眾對某一議題或問題有更深入的了解和討論。
民調可信嗎?
民意調查的結果數據隨處可見,尤其是政治性民調結果幾乎可說是天天在新聞上放送,對總統的滿意度下降了多少百分比,然而大家又信多少?
在景美市場的訪問中,我們了解到民眾對民調有一些普遍的觀點。大多數受訪者表示,他們對民調的可信度存有疑慮,主要原因是他們擔心政府可能會在調查中進行操控,以符合特定政治目標。
受訪者還提到,民意調查的結果通常不會對他們的投票意願產生影響。換句話說,他們的選擇通常受到更多因素的影響,例如候選人的政策立場和政府做事的認真與否,而不是單純依賴民調結果。
從訪問中我們可以得出的結論是,大多數民眾對民調持謹慎態度,並認為它們對他們的投票決策影響有限。
2024娛樂城的創新趨勢
隨著2024年的到來,娛樂城業界正經歷著一場革命性的變遷。這一年,娛樂城不僅僅是賭博和娛樂的代名詞,更成為了科技創新和用戶體驗的集大成者。
首先,2024年的娛樂城極大地融合了最新的技術。增強現實(AR)和虛擬現實(VR)技術的引入,為玩家提供了沉浸式的賭博體驗。這種全新的遊戲方式不僅帶來視覺上的震撼,還為玩家創造了一種置身於真實賭場的感覺,而實際上他們可能只是坐在家中的沙發上。
其次,人工智能(AI)在娛樂城中的應用也達到了新高度。AI技術不僅用於增強遊戲的公平性和透明度,還在個性化玩家體驗方面發揮著重要作用。從個性化遊戲推薦到智能客服,AI的應用使得娛樂城更能滿足玩家的個別需求。
此外,線上娛樂城的安全性和隱私保護也獲得了顯著加強。隨著技術的進步,更加先進的加密技術和安全措施被用來保護玩家的資料和交易,從而確保一個安全可靠的遊戲環境。
2024年的娛樂城還強調負責任的賭博。許多平台採用了各種工具和資源來幫助玩家控制他們的賭博行為,如設置賭注限制、自我排除措施等,體現了對可持續賭博的承諾。
總之,2024年的娛樂城呈現出一個高度融合了技術、安全和負責任賭博的行業新面貌,為玩家提供了前所未有的娛樂體驗。隨著這些趨勢的持續發展,我們可以預見,娛樂城將不斷地創新和進步,為玩家帶來更多精彩和安全的娛樂選擇。
2024娛樂城的創新趨勢
隨著2024年的到來,娛樂城業界正經歷著一場革命性的變遷。這一年,娛樂城不僅僅是賭博和娛樂的代名詞,更成為了科技創新和用戶體驗的集大成者。
首先,2024年的娛樂城極大地融合了最新的技術。增強現實(AR)和虛擬現實(VR)技術的引入,為玩家提供了沉浸式的賭博體驗。這種全新的遊戲方式不僅帶來視覺上的震撼,還為玩家創造了一種置身於真實賭場的感覺,而實際上他們可能只是坐在家中的沙發上。
其次,人工智能(AI)在娛樂城中的應用也達到了新高度。AI技術不僅用於增強遊戲的公平性和透明度,還在個性化玩家體驗方面發揮著重要作用。從個性化遊戲推薦到智能客服,AI的應用使得娛樂城更能滿足玩家的個別需求。
此外,線上娛樂城的安全性和隱私保護也獲得了顯著加強。隨著技術的進步,更加先進的加密技術和安全措施被用來保護玩家的資料和交易,從而確保一個安全可靠的遊戲環境。
2024年的娛樂城還強調負責任的賭博。許多平台採用了各種工具和資源來幫助玩家控制他們的賭博行為,如設置賭注限制、自我排除措施等,體現了對可持續賭博的承諾。
總之,2024年的娛樂城呈現出一個高度融合了技術、安全和負責任賭博的行業新面貌,為玩家提供了前所未有的娛樂體驗。隨著這些趨勢的持續發展,我們可以預見,娛樂城將不斷地創新和進步,為玩家帶來更多精彩和安全的娛樂選擇。
2024全新上線❰戰神賽特老虎機❱ – ATG賽特玩法說明介紹
❰戰神賽特老虎機❱是由ATG電子獨家開發的古埃及風格線上老虎機,在傳說中戰神賽特是「力量之神」與奈芙蒂斯女神結成連理,共同守護古埃及的奇幻秘寶,只有被選中的冒險者才能進入探險。
❰戰神賽特老虎機❱ – ATG賽特介紹
2024最新老虎機【戰神塞特】- ATG電子 X 富遊娛樂城
❰戰神賽特老虎機❱ – ATG電子
線上老虎機系統 : ATG電子
發行年分 : 2024年1月
最大倍數 : 51000倍
返還率 : 95.89%
支付方式 : 全盤倍數、消除掉落
最低投注金額 : 0.4元
最高投注金額 : 2000元
可否選台 : 是
可選台台數 : 350台
免費遊戲 : 選轉觸發+購買特色
❰戰神賽特老虎機❱ 賠率說明
戰神塞特老虎機賠率算法非常簡單,玩家們只需要不斷的轉動老虎機,成功消除物件即可贏分,得分賠率依賠率表計算。
當盤面上沒有物件可以消除時,倍數符號將會相加形成總倍數!該次旋轉的總贏分即為 : 贏分 X 總倍數。
積分方式如下 :
贏分=(單次押注額/20) X 物件賠率
EX : 單次押注額為1,盤面獲得12個戰神賽特倍數符號法老魔眼
贏分= (1/20) X 1000=50
以下為各個得分符號數量之獎金賠率 :
得分符號 獎金倍數 得分符號 獎金倍數
戰神賽特倍數符號聖甲蟲 6 2000
5 100
4 60 戰神賽特倍數符號黃寶石 12+ 200
10-11 30
8-9 20
戰神賽特倍數符號荷魯斯之眼 12+ 1000
10-11 500
8-9 200 戰神賽特倍數符號紅寶石 12+ 160
10-11 24
8-9 16
戰神賽特倍數符號眼鏡蛇 12+ 500
10-11 200
8-9 50 戰神賽特倍數符號紫鑽石 12+ 100
10-11 20
8-9 10
戰神賽特倍數符號神箭 12+ 300
10-11 100
8-9 40 戰神賽特倍數符號藍寶石 12+ 80
10-11 18
8-9 8
戰神賽特倍數符號屠鐮刀 12+ 240
10-11 40
8-9 30 戰神賽特倍數符號綠寶石 12+ 40
10-11 15
8-9 5
❰戰神賽特老虎機❱ 賠率說明(橘色數值為獲得數量、黑色數值為得分賠率)
ATG賽特 – 特色說明
ATG賽特 – 倍數符號獎金加乘
玩家們在看到盤面上出現倍數符號時,務必把握機會加速轉動ATG賽特老虎機,倍數符號會隨機出現2到500倍的隨機倍數。
當盤面無法在消除時,這些倍數總和會相加,乘上當時累積之獎金,即為最後得分總額。
倍數符號會出現在主遊戲和免費遊戲當中,玩家們千萬別錯過這個可以瞬間將得獎金額拉高的好機會!
ATG賽特 – 倍數符號獎金加乘
ATG賽特 – 倍數符號圖示
ATG賽特 – 進入神秘金字塔開啟免費遊戲
戰神賽特倍數符號聖甲蟲
❰戰神賽特老虎機❱ 免費遊戲符號
在古埃及神話中,聖甲蟲又稱為「死亡之蟲」,它被當成了天球及重生的象徵,守護古埃及的奇幻秘寶。
當玩家在盤面上,看見越來越多的聖甲蟲時,千萬不要膽怯,只需在牌面上斬殺4~6個ATG賽特免費遊戲符號,就可以進入15場免費遊戲!
在免費遊戲中若轉出3~6個聖甲蟲免費遊戲符號,可額外獲得5次免費遊戲,最高可達100次。
當玩家的累積贏分且盤面有倍數物件時,盤面上的所有倍數將會加入總倍數!
ATG賽特 – 選台模式贏在起跑線
為避免神聖的寶物被盜墓者奪走,富有智慧的法老王將金子塔內佈滿迷宮,有的設滿機關讓盜墓者寸步難行,有的暗藏機關可以直接前往存放神秘寶物的暗房。
ATG賽特老虎機設有350個機檯供玩家選擇,這是連魔龍老虎機、忍老虎機都給不出的機台數量,為的就是讓玩家,可以隨時進入神秘的古埃及的寶藏聖域,挖掘長眠已久的神祕寶藏。
【戰神塞特老虎機】選台模式
❰戰神賽特老虎機❱ 選台模式
ATG賽特 – 購買免費遊戲挖掘秘寶
玩家們可以使用當前投注額的100倍購買免費遊戲!進入免費遊戲再也不是虛幻。獎勵與一般遊戲相同,且購買後遊戲將自動開始,直到場次和獎金發放完畢為止。
有購買免費遊戲需求的玩家們,立即點擊「開始」,啟動神秘金字塔裡的古埃及祕寶吧!
【戰神塞特老虎機】購買特色
❰戰神賽特老虎機❱ 購買特色
戰神賽特試玩推薦
看完了❰戰神賽特老虎機❱介紹之後,玩家們是否也蓄勢待發要進入古埃及的世界,一探神奇秘寶探險之旅。
本次ATG賽特與線上娛樂城推薦第一名的富遊娛樂城合作,只需要加入會員,即可領取到168體驗金,免費試玩420轉!
2024娛樂城No.1 – 富遊娛樂城介紹
2024 年 1 月 5 日
|
娛樂城, 現金版娛樂城
富遊娛樂城是無論老手、新手,都非常推薦的線上博奕,在2024娛樂城當中扮演著多年來最來勢洶洶的一匹黑馬,『人性化且精緻的介面,遊戲種類眾多,超級多的娛樂城優惠,擁有眾多與會員交流遊戲的群組』是一大特色。
富遊娛樂城擁有歐洲馬爾他(MGA)和菲律賓政府競猜委員會(PAGCOR)頒發的合法執照。
註冊於英屬維爾京群島,受國際行業協會認可的合法公司。
我們的中心思想就是能夠帶領玩家遠詐騙黑網,讓大家安心放心的暢玩線上博弈,娛樂城也受各大部落客、IG網紅、PTT論壇,推薦討論,富遊娛樂城沒有之一,絕對是線上賭場玩家的第一首選!
富遊娛樂城介面 / 2024娛樂城NO.1
富遊娛樂城簡介
品牌名稱 : 富遊RG
創立時間 : 2019年
存款速度 : 平均15秒
提款速度 : 平均5分
單筆提款金額 : 最低1000-100萬
遊戲對象 : 18歲以上男女老少皆可
合作廠商 : 22家遊戲平台商
支付平台 : 各大銀行、各大便利超商
支援配備 : 手機網頁、電腦網頁、IOS、安卓(Android)
富遊娛樂城遊戲品牌
真人百家 — 歐博真人、DG真人、亞博真人、SA真人、OG真人
體育投注 — SUPER體育、鑫寶體育、亞博體育
電競遊戲 — 泛亞電競
彩票遊戲 — 富遊彩票、WIN 539
電子遊戲 —ZG電子、BNG電子、BWIN電子、RSG電子、好路GR電子
棋牌遊戲 —ZG棋牌、亞博棋牌、好路棋牌、博亞棋牌
捕魚遊戲 —ZG捕魚、RSG捕魚、好路GR捕魚、亞博捕魚
富遊娛樂城優惠活動
每日任務簽到金666
富遊VIP全面啟動
復酬金活動10%優惠
日日返水
新會員好禮五選一
首存禮1000送1000
免費體驗金$168
富遊娛樂城APP
步驟1 : 開啟網頁版【富遊娛樂城官網】
步驟2 : 點選上方(下載app),會跳出下載與複製連結選項,點選後跳轉。
步驟3 : 跳轉後點選(安裝),並點選(允許)操作下載描述檔,跳出下載描述檔後點選關閉。
步驟4 : 到手機設置>一般>裝置管理>設定描述檔(富遊)安裝,即可完成安裝。
富遊娛樂城常見問題FAQ
富遊娛樂城詐騙?
黑網詐騙可細分兩種,小出大不出及純詐騙黑網,我們可從品牌知名度經營和網站架設畫面分辨來簡單分辨。
富遊娛樂城會出金嗎?
如上面提到,富遊是在做一個品牌,為的是能夠保證出金,和帶領玩家遠離黑網,而且還有DUKER娛樂城出金認證,所以各位能夠放心富遊娛樂城為正出金娛樂城。
富遊娛樂城出金延遲怎麼辦?
基本上只要是公司系統問提造成富遊娛樂城會員無法在30分鐘成功提款,富遊娛樂城會即刻派送補償金,表達誠摯的歉意。
富遊娛樂城結論
富遊娛樂城安心玩,評價4.5顆星。如果還想看其他娛樂城推薦的,可以來娛樂城推薦尋找喔。
2024娛樂城No.1 – 富遊娛樂城介紹
2024 年 1 月 5 日
|
娛樂城, 現金版娛樂城
富遊娛樂城是無論老手、新手,都非常推薦的線上博奕,在2024娛樂城當中扮演著多年來最來勢洶洶的一匹黑馬,『人性化且精緻的介面,遊戲種類眾多,超級多的娛樂城優惠,擁有眾多與會員交流遊戲的群組』是一大特色。
富遊娛樂城擁有歐洲馬爾他(MGA)和菲律賓政府競猜委員會(PAGCOR)頒發的合法執照。
註冊於英屬維爾京群島,受國際行業協會認可的合法公司。
我們的中心思想就是能夠帶領玩家遠詐騙黑網,讓大家安心放心的暢玩線上博弈,娛樂城也受各大部落客、IG網紅、PTT論壇,推薦討論,富遊娛樂城沒有之一,絕對是線上賭場玩家的第一首選!
富遊娛樂城介面 / 2024娛樂城NO.1
富遊娛樂城簡介
品牌名稱 : 富遊RG
創立時間 : 2019年
存款速度 : 平均15秒
提款速度 : 平均5分
單筆提款金額 : 最低1000-100萬
遊戲對象 : 18歲以上男女老少皆可
合作廠商 : 22家遊戲平台商
支付平台 : 各大銀行、各大便利超商
支援配備 : 手機網頁、電腦網頁、IOS、安卓(Android)
富遊娛樂城遊戲品牌
真人百家 — 歐博真人、DG真人、亞博真人、SA真人、OG真人
體育投注 — SUPER體育、鑫寶體育、亞博體育
電競遊戲 — 泛亞電競
彩票遊戲 — 富遊彩票、WIN 539
電子遊戲 —ZG電子、BNG電子、BWIN電子、RSG電子、好路GR電子
棋牌遊戲 —ZG棋牌、亞博棋牌、好路棋牌、博亞棋牌
捕魚遊戲 —ZG捕魚、RSG捕魚、好路GR捕魚、亞博捕魚
富遊娛樂城優惠活動
每日任務簽到金666
富遊VIP全面啟動
復酬金活動10%優惠
日日返水
新會員好禮五選一
首存禮1000送1000
免費體驗金$168
富遊娛樂城APP
步驟1 : 開啟網頁版【富遊娛樂城官網】
步驟2 : 點選上方(下載app),會跳出下載與複製連結選項,點選後跳轉。
步驟3 : 跳轉後點選(安裝),並點選(允許)操作下載描述檔,跳出下載描述檔後點選關閉。
步驟4 : 到手機設置>一般>裝置管理>設定描述檔(富遊)安裝,即可完成安裝。
富遊娛樂城常見問題FAQ
富遊娛樂城詐騙?
黑網詐騙可細分兩種,小出大不出及純詐騙黑網,我們可從品牌知名度經營和網站架設畫面分辨來簡單分辨。
富遊娛樂城會出金嗎?
如上面提到,富遊是在做一個品牌,為的是能夠保證出金,和帶領玩家遠離黑網,而且還有DUKER娛樂城出金認證,所以各位能夠放心富遊娛樂城為正出金娛樂城。
富遊娛樂城出金延遲怎麼辦?
基本上只要是公司系統問提造成富遊娛樂城會員無法在30分鐘成功提款,富遊娛樂城會即刻派送補償金,表達誠摯的歉意。
富遊娛樂城結論
富遊娛樂城安心玩,評價4.5顆星。如果還想看其他娛樂城推薦的,可以來娛樂城推薦尋找喔。
Дома АВС – Ваш уютный уголок
Мы строим не просто дома, мы создаем пространство, где каждый уголок будет наполнен комфортом и радостью жизни. Наш приоритет – не просто предоставить место для проживания, а создать настоящий дом, где вы будете чувствовать себя счастливыми и уютно.
В нашем информационном разделе „ПРОЕКТЫ” вы всегда найдете вдохновение и новые идеи для строительства вашего будущего дома. Мы постоянно работаем над тем, чтобы предложить вам самые инновационные и стильные проекты.
Мы убеждены, что основа хорошего дома – это его дизайн. Поэтому мы предоставляем услуги опытных дизайнеров-архитекторов, которые помогут вам воплотить все ваши идеи в жизнь. Наши архитекторы и персональные консультанты всегда готовы поделиться своим опытом и предложить функциональные и комфортные решения для вашего будущего дома.
Мы стремимся сделать весь процесс строительства максимально комфортным для вас. Наша команда предоставляет детализированные сметы, разрабатывает четкие этапы строительства и осуществляет контроль качества на каждом этапе.
Для тех, кто ценит экологичность и близость к природе, мы предлагаем деревянные дома премиум-класса. Используя клееный брус и оцилиндрованное бревно, мы создаем уникальные и здоровые условия для вашего проживания.
Тем, кто предпочитает надежность и многообразие форм, мы предлагаем дома из камня, блоков и кирпичной кладки.
Для практичных и ценящих свое время людей у нас есть быстровозводимые каркасные дома и эконом-класса. Эти решения обеспечат вас комфортным проживанием в кратчайшие сроки.
С Домами АВС создайте свой уютный уголок, где каждый момент жизни будет наполнен радостью и удовлетворением
**娛樂城與線上賭場:現代娛樂的轉型與未來**
在當今數位化的時代,”娛樂城”和”線上賭場”已成為現代娛樂和休閒生活的重要組成部分。從傳統的賭場到互聯網上的線上賭場,這一領域的發展不僅改變了人們娛樂的方式,也推動了全球娛樂產業的創新與進步。
**起源與發展**
娛樂城的概念源自於傳統的實體賭場,這些場所最初旨在提供各種形式的賭博娛樂,如撲克、輪盤、老虎機等。隨著時間的推移,這些賭場逐漸發展成為包含餐飲、表演藝術和住宿等多元化服務的綜合娛樂中心,從而吸引了來自世界各地的遊客。
隨著互聯網技術的飛速發展,線上賭場應運而生。這種新型態的賭博平台讓使用者可以在家中或任何有互聯網連接的地方,享受賭博遊戲的樂趣。線上賭場的出現不僅為賭博愛好者提供了更多便利與選擇,也大大擴展了賭博產業的市場範圍。
**特點與魅力**
娛樂城和線上賭場的主要魅力在於它們能提供多樣化的娛樂選項和高度的可訪問性。無論是實體的娛樂城還是虛擬的線上賭場,它們都致力於創造一個充滿樂趣和刺激的環境,讓人們可以從日常生活的壓力中短暫逃脫。
此外,線上賭場通過提供豐富的遊戲選擇、吸引人的獎金方案以及便捷的支付系統,成功地吸引了全球範圍內的用戶。這些平台通常具有高度的互動性和社交性,使玩家不僅能享受遊戲本身,還能與來自世界各地的其他玩家交流。
**未來趨勢**
隨著技術的不斷進步和用戶需求的不斷演變,娛樂城和線上賭場的未來發展呈現出多元化的趨勢。一方面,虛
擬現實(VR)和擴增現實(AR)技術的應用,有望為線上賭場帶來更加沉浸式和互動式的遊戲體驗。另一方面,對於實體娛樂城而言,將更多地注重提供綜合性的休閒體驗,結合賭博、娛樂、休閒和旅遊等多個方面,以滿足不同客群的需求。
此外,隨著對負責任賭博的認識加深,未來娛樂城和線上賭場在提供娛樂的同時,也將更加注重促進健康的賭博行為和保護用戶的安全。
總之,娛樂城和線上賭場作為現代娛樂生活的一部分,隨著社會的發展和技術的進步,將繼續演化和創新,為人們提供更多的樂趣和便利。這一領域的未來發展無疑充滿了無限的可能性和機遇。
Скрытая сеть, является, скрытую, сеть, на, сети, подключение к этой сети, реализуется, через, определенные, приложения а также, инструменты, предоставляющие, конфиденциальность пользовательские данных. Один из, подобных, средств, считается, Тор браузер, который, гарантирует, приватное, подключение к сети, в даркнет. При помощи, его, сетевые пользователи, могут, незаметно, посещать, сайты, не индексируемые, традиционными, поисками, позволяя таким образом, условия, для проведения, разнообразных, запрещенных операций.
Киберторговая площадка, в свою очередь, часто ассоциируется с, скрытой сетью, как, рынок, для осуществления обмена, криминалитетом. Здесь, есть возможность, приобрести, различные, запрещенные, услуги, начиная от, препаратов и огнестрельного оружия, доходя до, хакерскими действиями. Платформа, гарантирует, крупную долю, шифрования, и, анонимности, что, создает, ее, желанной, для тех, кого, намерен, уклониться от, негативных последствий, со стороны органов порядка.
Даркнет, представляет собой, скрытую, платформу, на, сети, подключение к этой сети, реализуется, путем, специальные, программы плюс, технологии, обеспечивающие, скрытность пользовательские данных. Один из, таких, средств, считается, The Onion Router, который, гарантирует, приватное, подключение, к даркнету. С помощью, его, пользователи, имеют шанс, безопасно, обращаться к, интернет-ресурсы, не отображаемые, обычными, поисковыми системами, создавая тем самым, условия, для организации, разнообразных, запрещенных деятельностей.
Кракен, соответственно, часто упоминается в контексте, даркнетом, как, площадка, для осуществления обмена, киберпреступниками. Здесь, имеется возможность, купить, разнообразные, запрещенные, товары, начиная, наркотических средств и огнестрельного оружия, доходя до, хакерскими услугами. Система, предоставляет, высокую степень, криптографической защиты, и также, защиты личной информации, это, предоставляет, ее, желанной, для тех, кто, стремится, уклониться от, негативных последствий, со стороны органов порядка.
Watches World
В пределах века цифровых технологий, в условиях, когда онлайн границы стекаются с реальностью, не рекомендуется игнорировать присутствие угроз в даркнете. Одной из таких угроз является blacksprut – выражение, превратившийся символом противозаконной, вредоносной деятельности в скрытых уголках интернета.
Blacksprut, будучи элементом подпольной сети, представляет значительную угрозу для безопасности в сети и личной безопасности пользователей. Этот темный уголок сети часто ассоциируется с незаконными сделками, торговлей запрещенными товарами и услугами, а также прочими противозаконными деяниями.
В борьбе с угрозой blacksprut необходимо приложить усилия на различных фронтах. Одним из важных направлений является совершенствование технологий цифровой безопасности. Развитие современных алгоритмов и технологий анализа данных позволит отслеживать и пресекать деятельность blacksprut в реальной ситуации.
Помимо инженерных мер, важна взаимодействие усилий правоохранительных органов на международном уровне. Международное сотрудничество в области кибербезопасности необходимо для успешного противодействия угрозам, связанным с blacksprut. Обмен знаний, разработка совместных стратегий и быстрые действия помогут уменьшить воздействие этой угрозы.
Образование и освещение также играют важное значение в борьбе с blacksprut. Повышение осведомленности пользователей о рисках подпольной сети и методах предупреждения становится неотъемлемой компонентом антиспампинговых мероприятий. Чем более осведомленными будут пользователи, тем меньше опасность попадания под влияние угрозы blacksprut.
В заключение, в борьбе с угрозой blacksprut необходимо скоординировать усилия как на цифровом, так и на нормативном уровнях. Это вызов, предполагающий совместных усилий граждан, служб безопасности и IT-компаний. Только совместными усилиями мы добьемся создания безопасного и надежного цифрового пространства для всех.
2024全新上線❰戰神賽特老虎機❱ – ATG賽特玩法說明介紹
❰戰神賽特老虎機❱是由ATG電子獨家開發的古埃及風格線上老虎機,在傳說中戰神賽特是「力量之神」與奈芙蒂斯女神結成連理,共同守護古埃及的奇幻秘寶,只有被選中的冒險者才能進入探險。
❰戰神賽特老虎機❱ – ATG賽特介紹
2024最新老虎機【戰神塞特】- ATG電子 X 富遊娛樂城
❰戰神賽特老虎機❱ – ATG電子
線上老虎機系統 : ATG電子
發行年分 : 2024年1月
最大倍數 : 51000倍
返還率 : 95.89%
支付方式 : 全盤倍數、消除掉落
最低投注金額 : 0.4元
最高投注金額 : 2000元
可否選台 : 是
可選台台數 : 350台
免費遊戲 : 選轉觸發+購買特色
❰戰神賽特老虎機❱ 賠率說明
戰神塞特老虎機賠率算法非常簡單,玩家們只需要不斷的轉動老虎機,成功消除物件即可贏分,得分賠率依賠率表計算。
當盤面上沒有物件可以消除時,倍數符號將會相加形成總倍數!該次旋轉的總贏分即為 : 贏分 X 總倍數。
積分方式如下 :
贏分=(單次押注額/20) X 物件賠率
EX : 單次押注額為1,盤面獲得12個戰神賽特倍數符號法老魔眼
贏分= (1/20) X 1000=50
以下為各個得分符號數量之獎金賠率 :
得分符號 獎金倍數 得分符號 獎金倍數
戰神賽特倍數符號聖甲蟲 6 2000
5 100
4 60 戰神賽特倍數符號黃寶石 12+ 200
10-11 30
8-9 20
戰神賽特倍數符號荷魯斯之眼 12+ 1000
10-11 500
8-9 200 戰神賽特倍數符號紅寶石 12+ 160
10-11 24
8-9 16
戰神賽特倍數符號眼鏡蛇 12+ 500
10-11 200
8-9 50 戰神賽特倍數符號紫鑽石 12+ 100
10-11 20
8-9 10
戰神賽特倍數符號神箭 12+ 300
10-11 100
8-9 40 戰神賽特倍數符號藍寶石 12+ 80
10-11 18
8-9 8
戰神賽特倍數符號屠鐮刀 12+ 240
10-11 40
8-9 30 戰神賽特倍數符號綠寶石 12+ 40
10-11 15
8-9 5
❰戰神賽特老虎機❱ 賠率說明(橘色數值為獲得數量、黑色數值為得分賠率)
ATG賽特 – 特色說明
ATG賽特 – 倍數符號獎金加乘
玩家們在看到盤面上出現倍數符號時,務必把握機會加速轉動ATG賽特老虎機,倍數符號會隨機出現2到500倍的隨機倍數。
當盤面無法在消除時,這些倍數總和會相加,乘上當時累積之獎金,即為最後得分總額。
倍數符號會出現在主遊戲和免費遊戲當中,玩家們千萬別錯過這個可以瞬間將得獎金額拉高的好機會!
ATG賽特 – 倍數符號獎金加乘
ATG賽特 – 倍數符號圖示
ATG賽特 – 進入神秘金字塔開啟免費遊戲
戰神賽特倍數符號聖甲蟲
❰戰神賽特老虎機❱ 免費遊戲符號
在古埃及神話中,聖甲蟲又稱為「死亡之蟲」,它被當成了天球及重生的象徵,守護古埃及的奇幻秘寶。
當玩家在盤面上,看見越來越多的聖甲蟲時,千萬不要膽怯,只需在牌面上斬殺4~6個ATG賽特免費遊戲符號,就可以進入15場免費遊戲!
在免費遊戲中若轉出3~6個聖甲蟲免費遊戲符號,可額外獲得5次免費遊戲,最高可達100次。
當玩家的累積贏分且盤面有倍數物件時,盤面上的所有倍數將會加入總倍數!
ATG賽特 – 選台模式贏在起跑線
為避免神聖的寶物被盜墓者奪走,富有智慧的法老王將金子塔內佈滿迷宮,有的設滿機關讓盜墓者寸步難行,有的暗藏機關可以直接前往存放神秘寶物的暗房。
ATG賽特老虎機設有350個機檯供玩家選擇,這是連魔龍老虎機、忍老虎機都給不出的機台數量,為的就是讓玩家,可以隨時進入神秘的古埃及的寶藏聖域,挖掘長眠已久的神祕寶藏。
【戰神塞特老虎機】選台模式
❰戰神賽特老虎機❱ 選台模式
ATG賽特 – 購買免費遊戲挖掘秘寶
玩家們可以使用當前投注額的100倍購買免費遊戲!進入免費遊戲再也不是虛幻。獎勵與一般遊戲相同,且購買後遊戲將自動開始,直到場次和獎金發放完畢為止。
有購買免費遊戲需求的玩家們,立即點擊「開始」,啟動神秘金字塔裡的古埃及祕寶吧!
【戰神塞特老虎機】購買特色
❰戰神賽特老虎機❱ 購買特色
日本にオンラインカジノおすすめランキング2024年最新版
2024おすすめのオンラインカジノ
オンラインカジノはパソコンでしか遊べないというのは、もう一昔前の話。現在はスマホやタブレットなどのモバイル端末からも、パソコンと変わらないクオリティでオンラインカジノを当たり前に楽しむことができるようになりました。
数あるモバイルカジノの中で、当サイトが厳選したトップ5カジノはこちら。
オンラインカジノおすすめ: コニベット(Konibet)
コニベットといえば、キャッシュバックや毎日もらえるリベートボーナスなど豪華ボーナスが満載!それに加えて低い出金条件も見どころです。さらにVIPレベルごとの還元率の高さも業界内で突出している点や、出金速度の速さなどトータルバランスの良さからもハイローラーの方にも好まれています。
カスタマーサポートは365日24時間稼働しているので、初心者の方にも安心してご利用いただけます。
さらに【業界初のオンラインポーカー】を導入!毎日トーナメントも開催されているので、早速参加しちゃいましょう!
RTP(還元率)公開や、入出金対応がスムーズで初心者向き
2000種類以上の豊富なゲーム数を誇り、スロットゲーム多数!
今なら$20の入金不要ボーナスと最大$650還元ボーナス!
8種類以上のライブカジノプロバイダー
業界初オンラインポーカーあり,日本利用者数No.1の安心のオンラインカジノメディア!
おすすめポイント
コニベットは、その豊富なボーナスと高還元率、そして安心のキャッシュバック制度で知られています。まず、新規登録者には入金不要の$20ボーナスが提供され、さらに初回入金時には最大$650の還元ボーナスが得られます。これらのキャンペーンはプレイヤーにとって大きな魅力となっています。
また、コニベットの特徴的な点は、VIP制度です。一度ロイヤルクラブになると、降格がなく、スロットリベートが1.5%という驚異の還元率を享受できます。これは他のオンラインカジノと比較しても非常に高い還元率です。さらに、常時週間損失キャッシュバックも行っているため、不運で負けてしまった場合でも取り返すチャンスがあります。これらの特徴から、コニベットはプレイヤーにとって非常に魅力的なオンラインカジノと言えるでしょう。
コニベット 無料会員登録をする
| コニベットのボーナス
コニベットは、新規登録者向けに20ドルの入金不要ボーナスを用意しています
コニベットカジノでは、限定で初回入金後に残高が1ドル未満になった場合、入金額の50%(最高500ドル)がキャッシュバックされる。キャッシュバック額に出金条件はないため、獲得後にすぐ出金することも可能です。
| コニベットの入金方法
入金方法 最低 / 最高入金
マスターカード 最低 : $20 / 最高 : $6,000
ジェイシービー 最低 : $20/ 最高 : $6,000
アメックス 最低 : $20 / 最高 : $6,000
アイウォレット 最低 : $20 / 最高 : $100,000
スティックペイ 最低 : $20 / 最高 : $100,000
ヴィーナスポイント 最低 : $20 / 最高 : $10,000
仮想通貨 最低 : $20 / 最高 : $100,000
銀行送金 最低 : $20 / 最高 : $10,000
| コニベット出金方法
出金方法 最低 |最高出金
アイウォレット 最低 : $40 / 最高 : なし
スティックぺイ 最低 : $40 / 最高 : なし
ヴィーナスポイント 最低 : $40 / 最高 : なし
仮想通貨 最低 : $40 / 最高 : なし
銀行送金 最低 : $40 / 最高 : なし
日本にオンラインカジノおすすめランキング2024年最新版
2024おすすめのオンラインカジノ
オンラインカジノはパソコンでしか遊べないというのは、もう一昔前の話。現在はスマホやタブレットなどのモバイル端末からも、パソコンと変わらないクオリティでオンラインカジノを当たり前に楽しむことができるようになりました。
数あるモバイルカジノの中で、当サイトが厳選したトップ5カジノはこちら。
オンラインカジノおすすめ: コニベット(Konibet)
コニベットといえば、キャッシュバックや毎日もらえるリベートボーナスなど豪華ボーナスが満載!それに加えて低い出金条件も見どころです。さらにVIPレベルごとの還元率の高さも業界内で突出している点や、出金速度の速さなどトータルバランスの良さからもハイローラーの方にも好まれています。
カスタマーサポートは365日24時間稼働しているので、初心者の方にも安心してご利用いただけます。
さらに【業界初のオンラインポーカー】を導入!毎日トーナメントも開催されているので、早速参加しちゃいましょう!
RTP(還元率)公開や、入出金対応がスムーズで初心者向き
2000種類以上の豊富なゲーム数を誇り、スロットゲーム多数!
今なら$20の入金不要ボーナスと最大$650還元ボーナス!
8種類以上のライブカジノプロバイダー
業界初オンラインポーカーあり,日本利用者数No.1の安心のオンラインカジノメディア!
おすすめポイント
コニベットは、その豊富なボーナスと高還元率、そして安心のキャッシュバック制度で知られています。まず、新規登録者には入金不要の$20ボーナスが提供され、さらに初回入金時には最大$650の還元ボーナスが得られます。これらのキャンペーンはプレイヤーにとって大きな魅力となっています。
また、コニベットの特徴的な点は、VIP制度です。一度ロイヤルクラブになると、降格がなく、スロットリベートが1.5%という驚異の還元率を享受できます。これは他のオンラインカジノと比較しても非常に高い還元率です。さらに、常時週間損失キャッシュバックも行っているため、不運で負けてしまった場合でも取り返すチャンスがあります。これらの特徴から、コニベットはプレイヤーにとって非常に魅力的なオンラインカジノと言えるでしょう。
コニベット 無料会員登録をする
| コニベットのボーナス
コニベットは、新規登録者向けに20ドルの入金不要ボーナスを用意しています
コニベットカジノでは、限定で初回入金後に残高が1ドル未満になった場合、入金額の50%(最高500ドル)がキャッシュバックされる。キャッシュバック額に出金条件はないため、獲得後にすぐ出金することも可能です。
| コニベットの入金方法
入金方法 最低 / 最高入金
マスターカード 最低 : $20 / 最高 : $6,000
ジェイシービー 最低 : $20/ 最高 : $6,000
アメックス 最低 : $20 / 最高 : $6,000
アイウォレット 最低 : $20 / 最高 : $100,000
スティックペイ 最低 : $20 / 最高 : $100,000
ヴィーナスポイント 最低 : $20 / 最高 : $10,000
仮想通貨 最低 : $20 / 最高 : $100,000
銀行送金 最低 : $20 / 最高 : $10,000
| コニベット出金方法
出金方法 最低 |最高出金
アイウォレット 最低 : $40 / 最高 : なし
スティックぺイ 最低 : $40 / 最高 : なし
ヴィーナスポイント 最低 : $40 / 最高 : なし
仮想通貨 最低 : $40 / 最高 : なし
銀行送金 最低 : $40 / 最高 : なし
Теневые рынки и их незаконные деятельности представляют важную угрозу безопасности общества и являются объектом внимания правоохранительных органов по всему миру. В данной статье мы обсудим так называемые теневые рынки, где возможно покупать поддельные паспорта, и какие угрозы это несет для граждан и государства.
Теневые рынки представляют собой тайные интернет-площадки, на которых торгуется разнообразной незаконной продукцией и услугами. Среди этих услуг встречается и продажа поддельных документов, таких как паспорта. Эти рынки оперируют в теневой сфере интернета, используя зашифровывание и неизвестные платежные системы, чтобы оставаться непостижимыми для правоохранительных органов.
Покупка фальшивого паспорта на теневых рынках представляет серьезную угрозу национальной безопасности. похищение личных данных, подделывание документов и фальшивые идентификационные материалы могут быть использованы для совершения террористических актов, мошенничества и прочих преступлений.
Правоохранительные органы в различных странах активно борются с скрытыми рынками, проводя операции по выявлению и аресту тех, кто замешан в преступных действиях. Однако, по мере того как технологии становятся более сложными, эти рынки могут приспосабливаться и находить новые пути обхода законов.
Для обеспечения своей безопасности от рисков, связанных с скрытыми рынками, важно проявлять бдительность при обработке своих персональных данных. Это включает в себя остерегаться фишинговых атак, не предоставлять персональной информацией в недоверенных источниках и регулярно контролировать свои финансовые документы.
Кроме того, общество должно быть знающим о рисках и последствиях покупки поддельных удостоверений. Это способствует формированию осознанного и ответственного отношения к вопросам безопасности и поможет в борьбе с подпольными рынками. Поддержка законодательства, направленных на ужесточение наказаний за производство и сбыт поддельных удостоверений, также представляет важное направление в борьбе с этими преступлениями
Изготовление и использование копий банковских карт является противозаконной практикой, представляющей важную угрозу для безопасности финансовых систем и личных средств граждан. В данной статье мы рассмотрим риски и последствия покупки копий карт, а также как общество и правоохранительные органы борются с аналогичными преступлениями.
“Копии” карт — это поддельные подделки банковских карт, которые используются для неправомерных транзакций. Основной метод создания дубликатов — это угон данных с оригинальной карты и последующее кодирование этих данных на другую карту. Злоумышленники, предлагающие услуги по продаже клонов карт, обычно действуют в скрытой сфере интернета, где трудно выявить и пресечь их деятельность.
Покупка дубликатов карт представляет собой серьезное преступление, которое может повлечь за собой серьезные наказания. Покупатель также рискует стать соучастником мошенничества, что может привести к уголовной ответственности. Основные преступные действия в этой сфере включают в себя кражу личной информации, фальсификацию документов и, конечно же, финансовые махинации.
Банки и силовые структуры активно борются с преступлениями, связанными с дублированием карт. Банки внедряют современные технологии для определения подозрительных транзакций, а также предлагают услуги по обеспечению защиты для своих клиентов. Силовые структуры ведут оперативные действия и ловят тех, кто замешан в производстве и сбыте реплик карт.
Для обеспечения безопасности важно соблюдать бдительность при использовании банковских карт. Необходимо регулярно проверять выписки, избегать сомнительных сделок и следить за своей конфиденциальной информацией. Образование и информированность об угрозах также являются ключевыми средствами в борьбе с финансовыми преступлениями.
В заключение, использование дубликатов банковских карт — это незаконное и неприемлемое деяние, которое может привести к важным последствиям для тех, кто вовлечен в такую практику. Соблюдение мер защиты, осведомленность о возможных рисках и сотрудничество с органами порядка играют основополагающую роль в предотвращении и пресечении подобных преступлений