Potęgi o ujemnym wykładniku

Spis treści

• Podnoszenie liczby całkowitej do ujemnej potęgi
• Podnoszenie ułamka do ujemnej potęgi
• Podnoszenie liczby ujemnej do ujemnej potęgi
• Przykładowe zadania

Jak zawsze przy potęgach, najpierw trzy pojęcia, które będą nam potrzebne 🙂

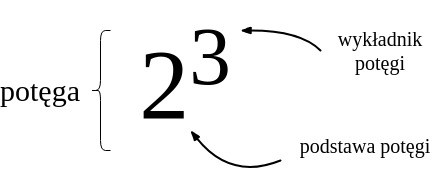
Podnoszenie liczby całkowitej do ujemnej potęgi

W kontekście potęgi o ujemnym wykładniku spotykamy się zazwyczaj z tym wzorem:

Jeśli , czyli podstawa potęgi, jest liczbą całkowitą (różną od zera), to ten wzór świetnie się sprawdza.

Przykłady:

Możemy stosować ten wzór także w drugą stronę, czyli zarówno przejść od dodatniego wykładnika do ujemnego:

jak i od ułamka do liczby całkowitej:

Generalnie wszystkie kombinacje dozwolone.

Podnoszenie ułamka do ujemnej potęgi

Gdy w podstawie mamy ułamek, również możemy stosować tamten wzór, ale moim zdaniem w tym przypadku za bardzo komplikuje on sprawę - zdecydowanie bardziej wolę ten:

W nim dużo wyraźniej widać, że ujemny wykładnik po prostu odwraca nam ułamek do góry nogami.

Przykłady:

Jak widzisz, przekształcenie polegało na tym, że zmieniłam znak wykładnika i odwróciłam ułamek do góry nogami.

Ten wzór, tak samo jak poprzedni, możemy stosować w drugą stronę, czyli przejść od dodatniego wykładnika do ujemnego:

To "stosowanie w drugą stronę" przyda nam się później przy rozwiązywaniu zadań.

Sprawa jest prosta, gdy mamy ułamek zwykły (czyli taki, w którym jasno widać, gdzie ma górę, a gdzie dół, więc zamiana góry z dołem nie stanowi wielkiej filozofii). Co jednak, gdy nie mamy ułamka zwykłego, tylko dziesiętny? Albo liczbę mieszaną?

W obu przypadkach musimy sobie ten ułamek zamienić na taki, który ma jasno zdefiniowane "górę" i "dół" - czyli właśnie na ułamek zwykły (swoją drogą warto to robić zawsze przy podnoszeniu ułamka do potęgi, nie tylko wtedy, gdy jest ona ujemna).

Tak to będzie wyglądało w przypadku ułamków dziesiętnych:

Czyli zamieniamy ułamek dziesiętny na zwykły, skracamy (jeśli się da) i odwracamy ułamek do góry nogami, zmieniając przy tym znak wykładnika.

W przypadku liczb mieszanych wygląda to tak:

Czyli znowu: zamieniamy na ułamek zwykły i odwracamy do góry nogami, zabierając minus z wykładnika.

Podnoszenie liczby ujemnej do ujemnej potęgi

To teraz bardzo ważne pytanie: co się zmienia, gdy potęgujemy liczbę ujemną? Odpowiedź brzmi: NIC. I to jest o tyle istotne, że wielu osobom włącza się automat "minus i minus daje plus" - to tutaj nie działa. Ujemny wykładnik nie zmienia znaku podstawy. Jedyne, co może zmienić jej znak, to parzysty wykładnik potęgi. Pokażę Ci to na dwóch przykładach (z nieparzystym i parzystym wykładnikiem):

Tutaj mamy nieparzysty wykładnik, więc po odwróceniu minus nadal zostaje.

Tu minus zniknął dlatego, że wykładnik był parzysty, a nie dlatego, że dwa minusy dały plus.

Na tej samej zasadzie ujemny wykładnik nie sprawi, że minus pojawi się w podstawie - jedno nie ma kompletnie wpływu na drugie. Ujemny wykładnik "odwraca liczbę do góry nogami" - nic więcej.

Przykładowe zadania

No to teraz gwóźdź programu, czyli odpowiedź na pytanie: "Jak i gdzie to wykorzystać?".

Pierwsze podstawowe zastosowanie to zadania typu "oblicz". Najprościej jest wtedy, gdy mamy po prostu liczbę podniesioną do ujemnej potęgi, tak jak tutaj:

W takim zadaniu mamy do wykonania dwa kroki. Krok pierwszy: pozbycie się minusa w wykładniku.

Krok drugi: potęgowanie.

No i tyle 🙂

Częściej jednak potęgi o ujemnym wykładniku idą w parze z działaniami na potęgach. Spójrz na to zadanie:

Możemy łatwo wykonać dzielenie potęg, o ile te potęgi mają albo te same podstawy, albo te same wykładniki. My nie mamy ani tego, ani tego. Możemy jednak zauważyć, że do uzyskania takich samych podstaw potrzebujemy jedynie odwrócenia ułamka do góry nogami, a to możemy łatwo zrobić.

Teraz, gdy mamy takie same podstawy, możemy wykonać dzielenie potęg.

No a to już jest coś, co możemy łatwo obliczyć.

Następne zadanie:

Tu z kolei możemy zobaczyć, że niewiele nam brakuje do uzyskania takich samych wykładników. Wystarczy, że pozbędziemy się minusa.

Teraz mamy takie same wykładniki, więc możemy wykonać mnożenie potęg.

Następny krok to wykonanie działań w nawiasach.

No i na koniec zostaje nam potęgowanie.

W dwóch poprzednich zadaniach było dość łatwo zauważyć, co potrzebujemy zrobić. Czasami jednak może to nie być widoczne na pierwszy rzut oka. Tak się dzieje na przykład wtedy, gdy mamy liczby mieszane.

Póki co szału nie ma, ale zobacz co się stanie, gdy zamienimy liczbę mieszaną na ułamek zwykły.

Teraz już widać, że niewiele nam brakuje do takich samych podstaw. Odwrócimy sobie drugi ułamek do góry nogami.

Teraz, gdy mamy takie same podstawy, możemy wykonać dzielenie potęg.

Innym przypadkiem, w którym nie widać na pierwszy rzut oka, co trzeba zrobić, są ułamki dziesiętne.

Zaczynamy od zamiany na ułamek zwykły.

Teraz już widać, że wystarczy odwrócić ułamek do góry nogami. Tutaj będziemy stosować wzór w drugą stronę, czyli dodamy minus do wykładnika.

Teraz możemy wykonać mnożenie potęg.

Zadanie typu "oblicz" nie jest jedynym zadaniem, jakie może nam się trafić - często jest tak, że oczekuje się od nas przekształcenia wyrażenia, a nie jego obliczenia. Tak jest w tym zadaniu.

To polecenie oznacza, że mamy tak przekształcić wyrażenie, by doprowadzić je do postaci " do jakiejś potęgi" - będziemy więc starali się jakoś tak zrobić, żeby te piątki się pojawiły. Lojalnie uprzedzam, że trochę nam to zajmie.

Zaczniemy od i zamienimy je na ułamek zwykły.

Jesteśmy na dobrej drodze do piątki, wystarczy już tylko zmienić znak wykładnika.

No i mamy. Teraz . Zaczniemy od tego, że zapiszemy jako .

Teraz pozbędziemy się ułamka, korzystając z tego wzoru (tylko w drugą stronę):

No i został nam dół. Na początku warto zauważyć, że jest podniesione do parzystej potęgi - a to oznacza, że bez wyrzutów sumienia możemy się tego minusa pozbyć.

Zamieniamy na .

Teraz wykonujemy potęgowanie potęgi, żeby pozbyć się nawiasów.

OK, mamy same piątki, teraz możemy wykonać działania na potęgach. Zacznę od uporządkowania góry.

Zostało nam pozbycie się ułamka.

Polecenie brzmiało "zapisz w postaci potęgi liczby ", więc nie wykonujemy potęgowania, tylko tak to zostawiamy.

Na koniec przykładowe zadanie maturalne.

Na początku zobaczmy, jakie mamy odpowiedzi. Po pierwsze możemy zauważyć, że naszym celem nie jest obliczenie, tylko przekształcenie wyrażenia. Po drugie widzimy, że w odpowiedziach nie ma nigdzie szesnastki - są za to dwójki. W pierwszych dwóch odpowiedziach w jawnej formie, natomiast w pozostałych dwóch - ukryte w dziesiątkach (). To jest dla nas podpowiedzią, że z szesnastki musimy jakoś zrobić dwójkę. A szczęśliwie dla nas, to .

Skorzystam teraz ze wzoru na potęgowanie potęgi:

Mamy zarówno różne podstawy, jak i różne potęgi, widać jednak, że do pełni szczęścia brakuje nam jedynie pozbycia się minusa.

Myślę, że na tym etapie domyślasz się już, która odpowiedź jest prawidłowa, ale dla porządku doprowadźmy rozwiązanie do końca 🙂 Zrobimy sobie z tego wyrażenia jeden ułamek.

No i na koniec wzór na dzielenie potęg.

Odpowiedź A.

Na sam koniec chcę podkreślić to, że nie zawsze, gdy mamy minus w wykładniku, musimy się tego minusa z automatu pozbywać. Faktycznie robimy to zawsze wtedy, gdy chcemy wykonać potęgowanie. Czyli gdy mamy i chcemy to obliczyć, to zawsze pozbywamy się najpierw minusa, a potem wykonujemy potęgowanie:

Natomiast gdy chcemy wykonać działania na potęgach, to niekoniecznie musimy pozbywać się minusa, a wręcz może to nam tylko skomplikować sprawę. Powiedzmy, że mamy takie działanie:

Tutaj mamy takie same podstawy, więc możemy bez problemu wykonać mnożenie potęg:

Natomiast gdybyśmy pozbyli się minusa i z szóstki zrobili ułamek, to tylko byśmy sobie te podstawy popsuli. Musimy po prostu patrzeć, co nam jest w danej sytuacji potrzebne i zastanowić się, czy pozbycie się minusa nam w tym pomoże, czy nie. Na początku będzie to trochę strzelanie w ciemno, ale z każdym kolejnym przykładem będzie to dla Ciebie coraz bardziej intuicyjne 🙂

Działania na potęgach - część 1
Potęgi o ułamkowym wykładniku