Zasady rozwiązywania nierówności liniowych są bardzo podobne do zasad rozwiązywania równań. Dlatego części wspólne omówię krótko, a bardziej skupię się na tym, co w nierównościach jest inne. Jeśli więc po przeczytaniu tego wpisu będziesz czuć niedosyt, to zapraszam Cię do posta o równaniach.
Najbardziej podstawowa nierówność wygląda na przykład tak: . Albo tak: . Pierwszą czytamy " jest większe od ", a drugą - " jest mniejsze bądź równe ". To jest postać, do której nierówność chcemy sprowadzić, gdy początkowo wygląda bardziej skomplikowanie.
Jeśli przy -ie stoi liczba, to podobnie jak przy równaniach, dzielimy nierówność obustronnie przez to, co przy tym -ie stoi. Ale uwaga: jeśli dzielimy (lub mnożymy) przez ujemną liczbę, to znak nierówności zmienia się na przeciwny. Powiedzmy, że mamy taką nierówność:
Dzielimy obustronnie przez . Jest to liczba dodatnia, więc znak nierówności się nie zmieni:
Możemy skrócić:
A teraz taka nierówność:
Dzielimy obustronnie przez . Jest to liczba ujemna, więc odwracamy znak nierówności:
Skracamy:
Podobnie sytuacja wygląda, gdy mamy taką nierówność:
Tak jak przy równaniach, możemy zamienić znaki po obu stronach, ale wtedy również musimy odwrócić znak nierówności (wynika to z faktu, że obustronna zamiana znaków to po prostu obustronne pomnożenie przez ).
Jeśli nierówność jest bardziej skomplikowana, to działamy tak samo, jak przy równaniach.
Przerzucam liczby na prawą stronę, a -y na lewą:
Porządkuję:
Dzielę obustronnie przez . Ponieważ jest to ujemna liczba, zmieniam znak nierówności na przeciwny:
Mamy dzielenie dwóch ujemnych liczb, zatem wynik będzie dodatni. Mogę więc usunąć minusy:
Zamienię jeszcze ułamek niewłaściwy na liczbę mieszaną:
Jeśli chodzi o przypadki z ułamkami, to tu, podobnie jak przy równaniach, mnożymy obustronnie przez wspólny mianownik. Weźmy na przykład taką nierówność:
Mamy tu dwa ułamki. Wspólny mianownik dla liczb i to , a więc mnożę nierówność obustronnie przez tę liczbę:
Mogę teraz sobie poskracać:
W ten sposób pozbyłam się ułamków:
Teraz pozbywam się nawiasów:
Przerzucam -y na lewą stronę, a liczby na prawą:
Porządkuję:
Teraz dzielę obustronnie przez . Zmieniam przy tym znak nierówności, bo jest to liczba ujemna:
Iloraz dwóch ujemnych liczb jest dodatni, więc pozbywam się minusów:
Na koniec zamieniam ułamek niewłaściwy na liczbę mieszaną:
W nierównościach z ułamkami jest jedna rzecz, która jest inna, niż w równaniach. Jeśli czytałeś post o rozwiązywaniu równań, to pewnie pamiętasz, że mówiłam, że jeśli po jednej i po drugiej stronie mamy tylko ułamek, to możemy "pomnożyć na skos" i w ten sposób tego ułamka się pozbyć. Przy nierównościach raczej bym to odradzała, bo bardzo łatwo jest pomylić strony. W takiej sytuacji moim zdaniem bezpieczniej jest po prostu pomnożyć nierówność przez wspólny mianownik, tak jak przy innych nierównościach z ułamkami. Weźmy na przykład taką nierówność:
Pomnożę nierówność obustronnie przez wspólny mianownik, czyli przez :
Teraz mogę sobie poskracać:
Dzięki temu pozbyliśmy się ułamków:
Przy pozbywaniu się ułamków koniecznie pamiętaj o nawiasach! Teraz będę się ich pozbywać:
Teraz przerzucam -y na lewą stronę, a liczby na prawą:
Porządkuję:
Dzielę obustronnie przez . Jest to dodatnia liczba, więc nie zmieniam znaku nierówności:
Jeśli chodzi o przekształcanie nierówności, to w zasadzie byłoby na tyle. Na tym jednak nasze rozwiązanie się nie kończy - rozwiązaniem nie jest bowiem pojedyncza liczba, jak w przypadku równania, ale cały zbiór liczb. Możemy go zapisać w postaci przedziału lub narysować na osi.
Powiedzmy, że mamy już nierówność doprowadzoną do końcowej postaci, czyli na przykład . Najpierw zaznaczymy sobie zbiór rozwiązań na osi. Aby to zrobić, najpierw rysujemy oś:

Następnie zaznaczamy na osi liczbę :

W naszym przypadku mamy tak zwaną nierówność ostrą - jest mniejszy (a nie mniejszy lub równy) . Dlatego nad szóstką rysujemy niezamalowane kółko:

Ponieważ jest mniejszy od szóstki, zaznaczamy liczby na lewo od tej niej:

To jest rozwiązanie w formie graficznej. Teraz zapiszemy je jeszcze w formie przedziału. Z rysunku możemy odczytać, że należy od minus nieskończoności do - i właśnie to zapiszemy, tylko przy użyciu symboli matematycznych:
Po obu stronach mamy okrągłe nawiasy. Po lewej stronie wynika to z tego, że przy nieskończonościach zawsze stawiamy okrągłe nawiasy. Po prawej stronie natomiast mamy okrągły nawias, ponieważ szóstka nie należy do tego przedziału ( jest mniejszy od , zatem nie może być szóstką) i właśnie przez okrągły nawias to oznaczamy.
Inny przykład:
Najpierw rysujemy oś:

Następnie zaznaczamy na niej liczbę :

Ponieważ mamy nieostrą nierówność (to znaczy, że jest większy lub równy), nad liczbą rysujemy zamalowane kółko:

Ze względu na to, że jest większy bądź równy , zaznaczamy na osi liczby większe od , czyli te po prawej stronie.

Mamy już rozwiązanie graficzne. Teraz zapiszemy je sobie w formie przedziału. Z rysunku możemy odczytać, że należy do zbioru liczb od do plus nieskończoności. Zapiszmy do sobie przy użyciu symboli matematycznych:
Zauważ, że tym razem mamy po lewej stronie "dzióbkowaty" nawias, a nie okrągły - to dlatego, że mamy nierówność nieostrą ( jest większy bądź równy ), z czego wynika, że liczba należy do tego przedziału. Aby to zaznaczyć, używamy właśnie takich "dzióbkowatych" nawiasów.
Podsumowując - jeśli mamy znak nierówności z taką kreseczką u dołu ( lub ), to na osi rysujemy zamalowane kółeczko i używamy "dzióbkowatych" nawiasów. Jeśli znak nierówności nie ma tej kreseczki ( lub ), to rysujemy niezamalowane kółeczko i używamy okrągłych nawiasów. Nawiasy przy nieskończonościach są zawsze okrągłe.
Może nam się zdarzyć taki przypadek, że dostaniemy do rozwiązania podwójną nierówność, na przykład taką:
W takiej sytuacji rozdzielamy ją sobie na dwie nierówności:
Każdą z nich przekształcamy osobno. Dla pierwszej będzie to wyglądało tak:
Natomiast dla drugiej tak:
Mamy więc dwie nierówności: oraz . Zaznaczymy je teraz na jednej osi liczbowej. Najpierw . Rysuję oś i zaznaczam na niej . Nad piątką rysuję niezamalowane kółeczko:

Następnie zaznaczam liczby większe od piątki, czyli te po prawej stronie (póki co jeszcze nie zamalowuję przedziału):

Teraz druga nierówność, czyli . Zaznaczam na osi dziewiątkę, a nad nią zamalowane kółeczko:
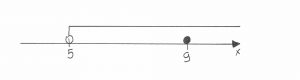
Następnie zaznaczam liczby mniejsze od dziewiątki, czyli te po lewej stronie:

Teraz wybieram część wspólną dla obu tych przedziałów:
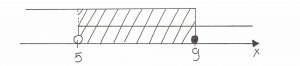
Będzie to przedział od (piątka nie należy do przedziału), do (dziewiątka należy do przedziału):
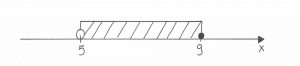
Zapiszę to teraz przy użyciu symboli matematycznych:
Przy liczbie, która nie należy do przedziału, stawiam okrągły nawias, a przy tej, która należy, stawiam "dzióbkowaty".
Mam nadzieję, że udało mi się to jasno wytłumaczyć 🙂