W poprzednim wpisie pokazywałam, jak wyznaczyć wartości funkcji trygonometrycznych dla kąta ostrego w trójkącie prostokątnym. Dziś będziemy wyznaczać wartości funkcji trygonometrycznych dla kąta od do .
Jak wiesz, możemy obliczyć wartości sinusa, cosinusa i tangensa, mając dane boki w trójkącie prostokątnym. Tam jednak kąt będzie zawsze mniejszy, niż . Tymczasem możemy obliczyć wartości tych funkcji dla dowolnie dużego kąta. Na poziomie podstawowym wymagają od Ciebie, byś umiał obliczyć te wartości dla kąta do . Jak to zrobić?
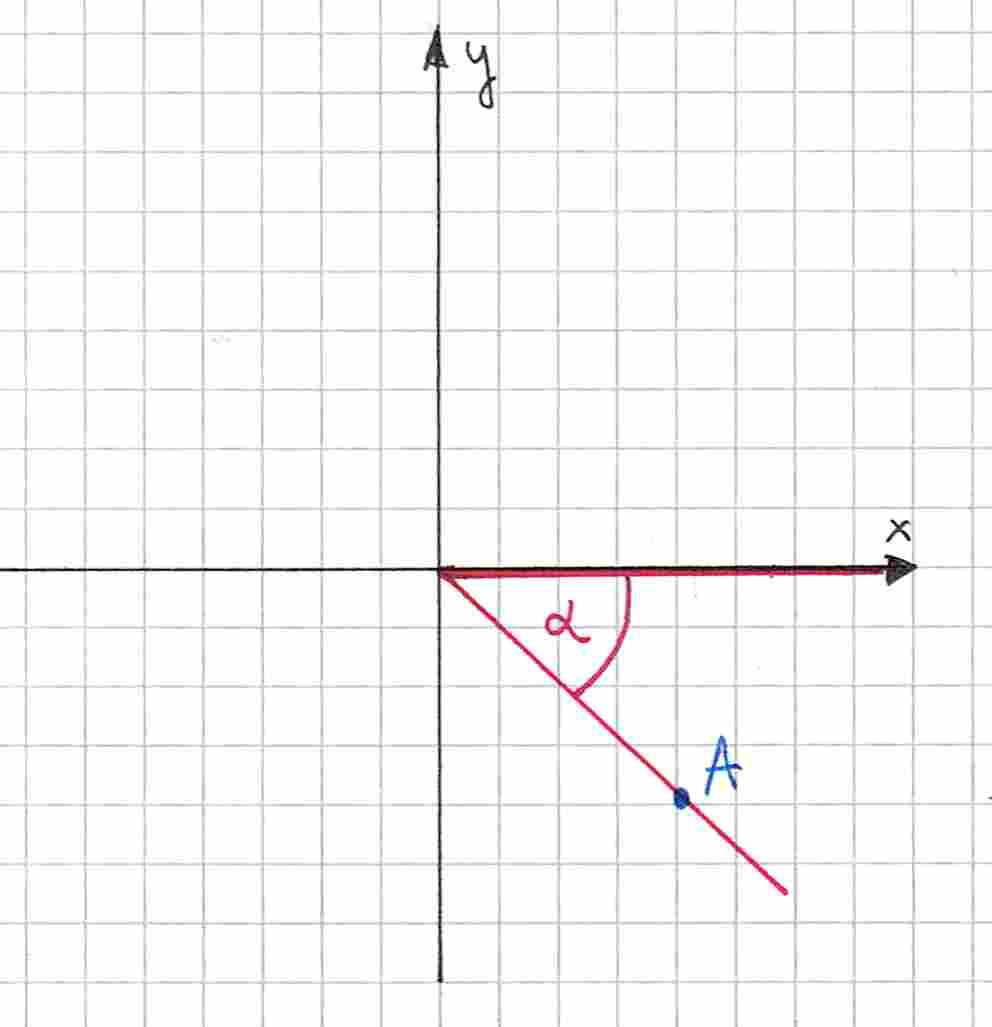
Taki kąt będzie osadzony w układzie współrzędnych. Jedno z jego ramion to dodatnia część osi , natomiast drugie ramię może być skierowane dowolnie. Wierzchołek kąta znajduje się w środku układu współrzędnych. Wygląda to mniej więcej tak:
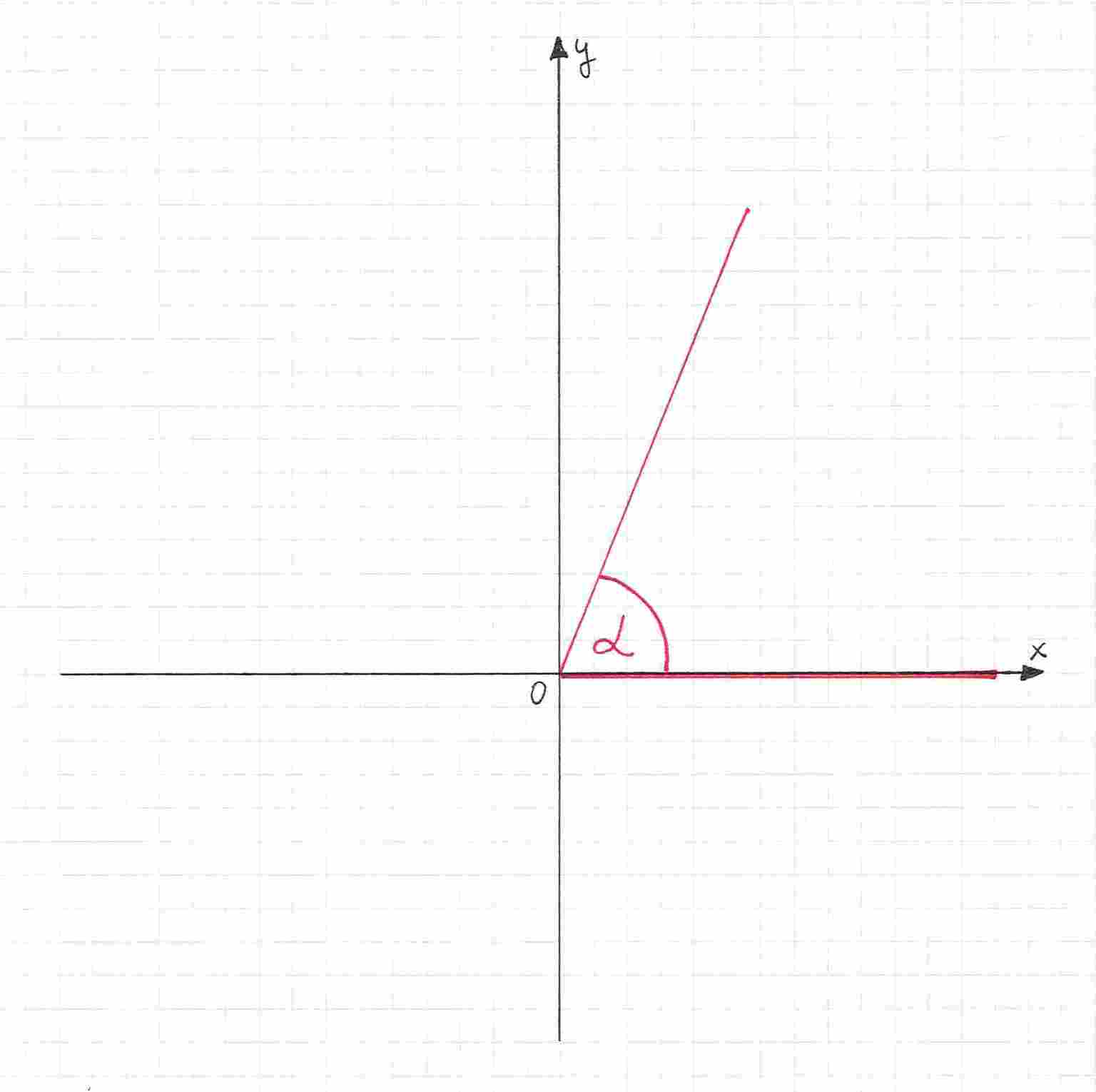
Aby wyznaczyć wartości funkcji trygonometrycznych dla tego kąta, potrzebujemy punktu, który będzie leżał na tym drugim ramieniu kąta. Musimy znać jego współrzędne.
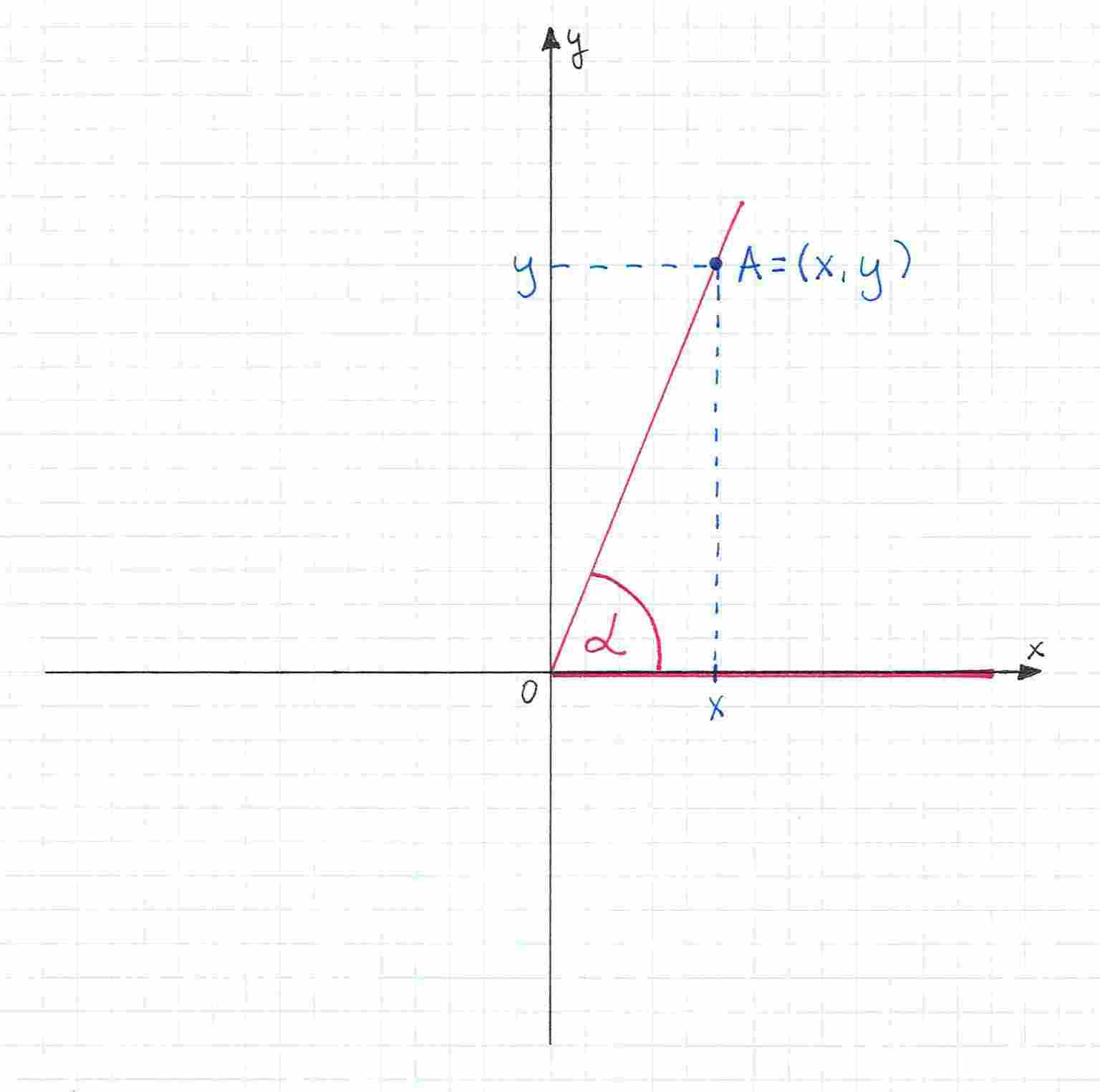
Musimy też znać odległość od punktu do środka układu współrzędnych. Oznaczamy ją jako i obliczamy za pomocą wzoru:
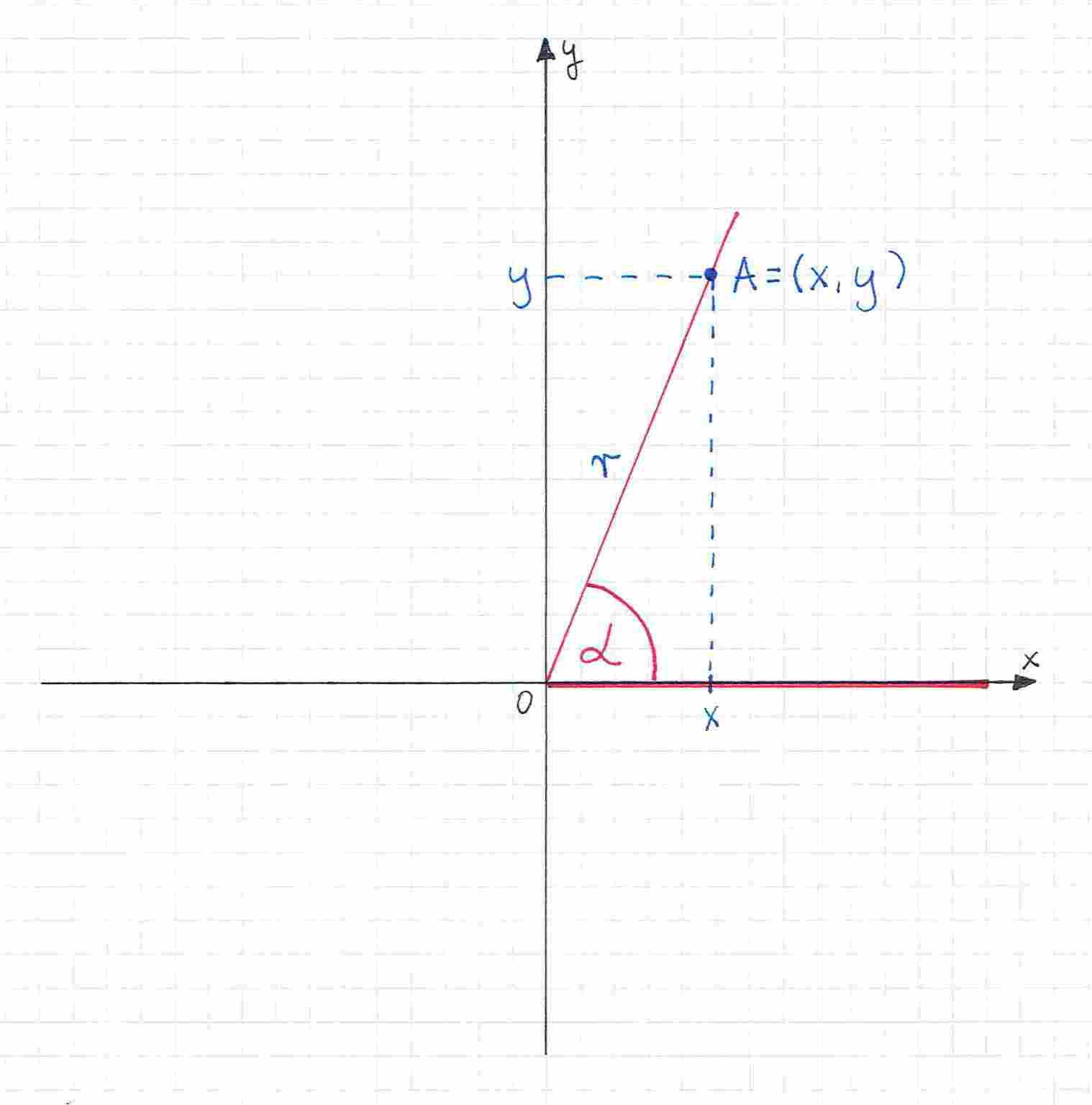
Gdy już to wszystko mamy, to wzory na sinus, cosinus i tangens kąta wyglądają następująco:
Na pokazanym przeze mnie rysunku ramię kąta znajduje się w pierwszej ćwiartce układu współrzędnych. Ponieważ jednak obowiązują nas kąty do , ramię to może też leżeć w drugiej ćwiartce, tak jak tutaj:
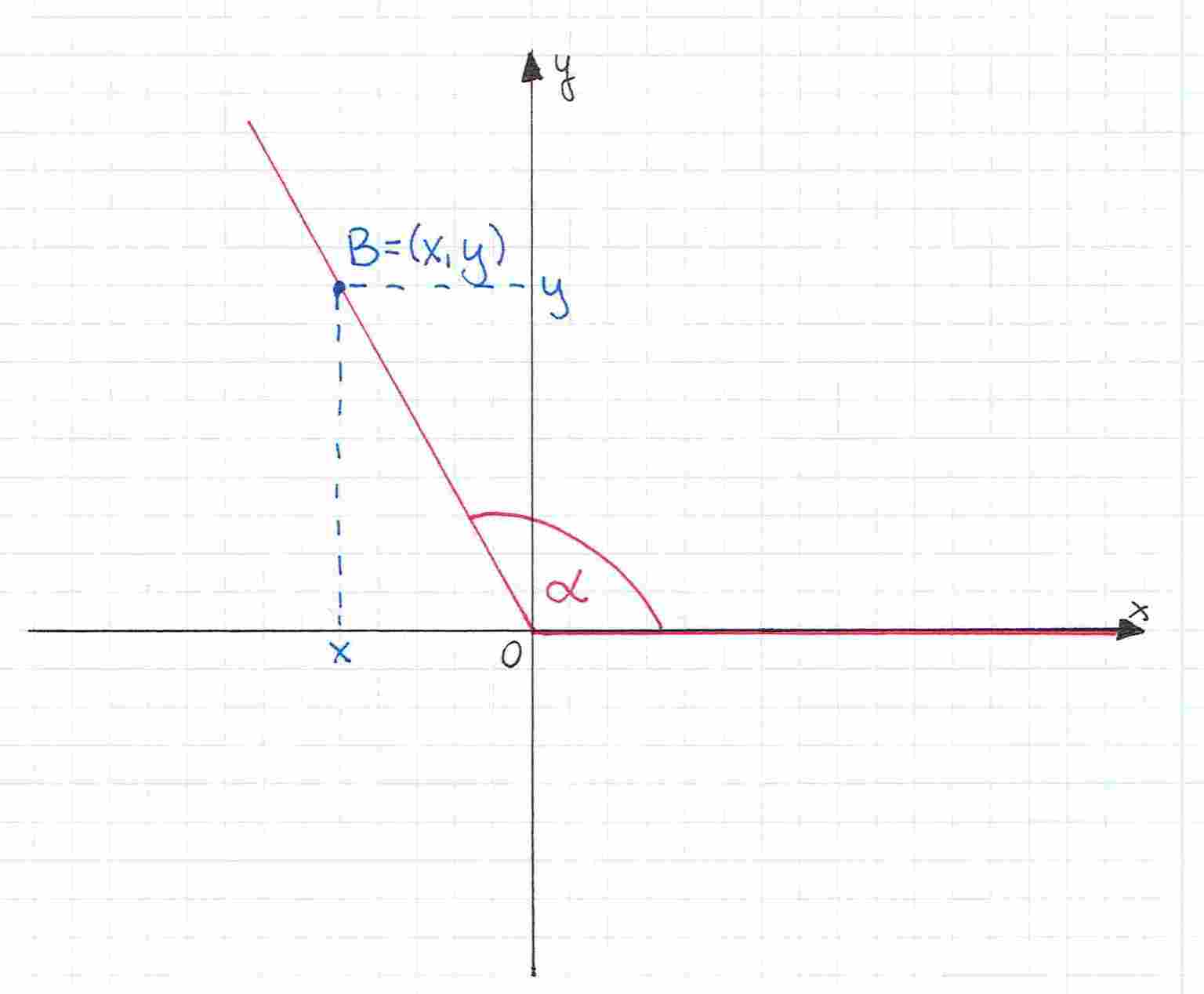
Przećwiczmy obliczanie wartości funkcji w obu przypadkach:
Wyznacz sinus, cosinus oraz tangens kąta zaznaczonego na rysunku.
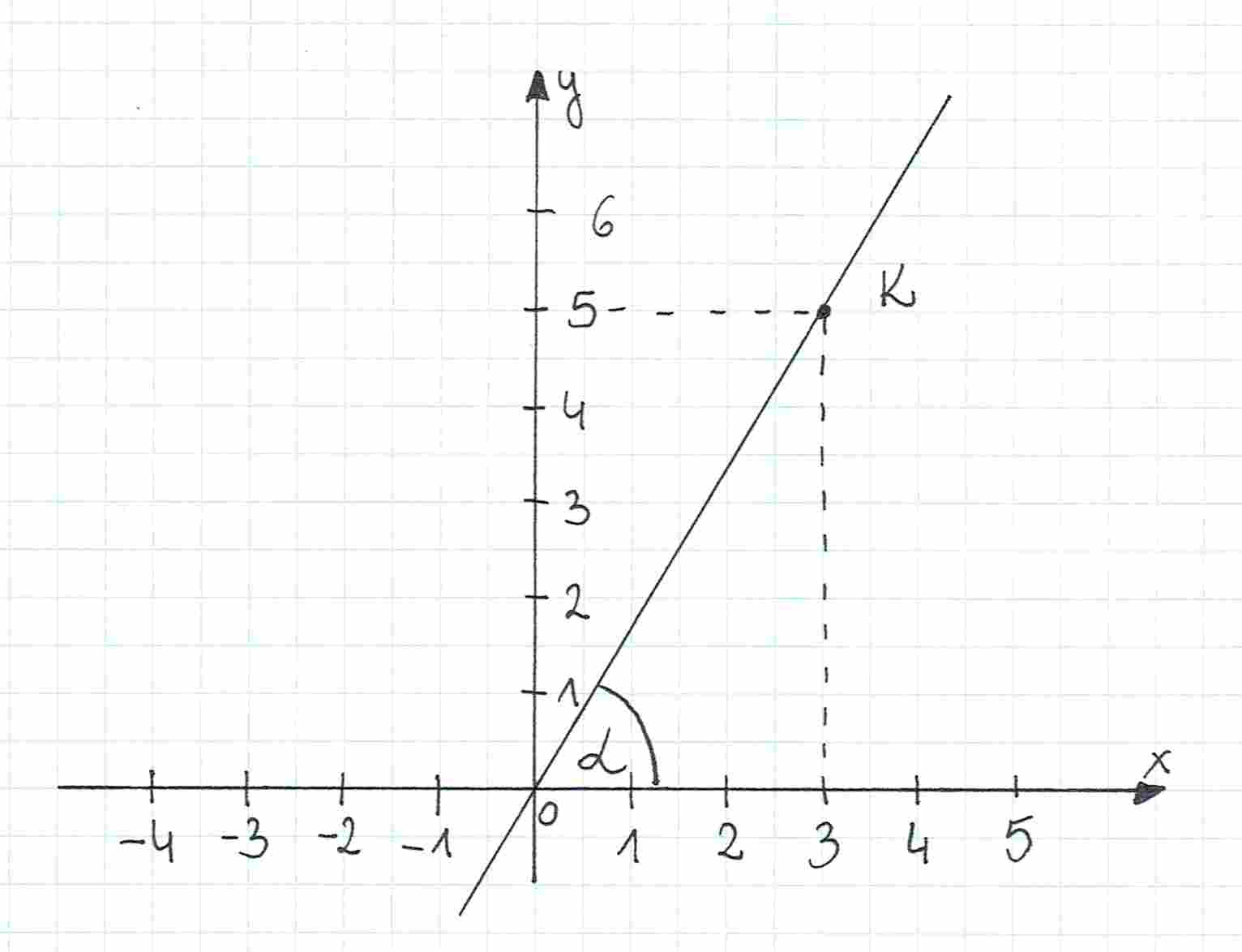
Potrzebujemy współrzędnych punktu . Współrzędna -owa to , a -owa to , tak więc
Teraz potrzebujemy długości . Obliczymy ją ze wzoru:
Podstawiamy do niego współrzędne punktu :
Teraz możemy wyznaczyć wartości funkcji trygonometrycznych:
Przy obliczaniu wartości sinusa i cosinusa dodatkowo usunęłam niewymierność z mianownika.
Teraz przećwiczymy to samo, tylko z ramieniem kąta w drugiej ćwiartce układu współrzędnych:
Wyznacz sinus, cosinus oraz tangens kąta zaznaczonego na rysunku.
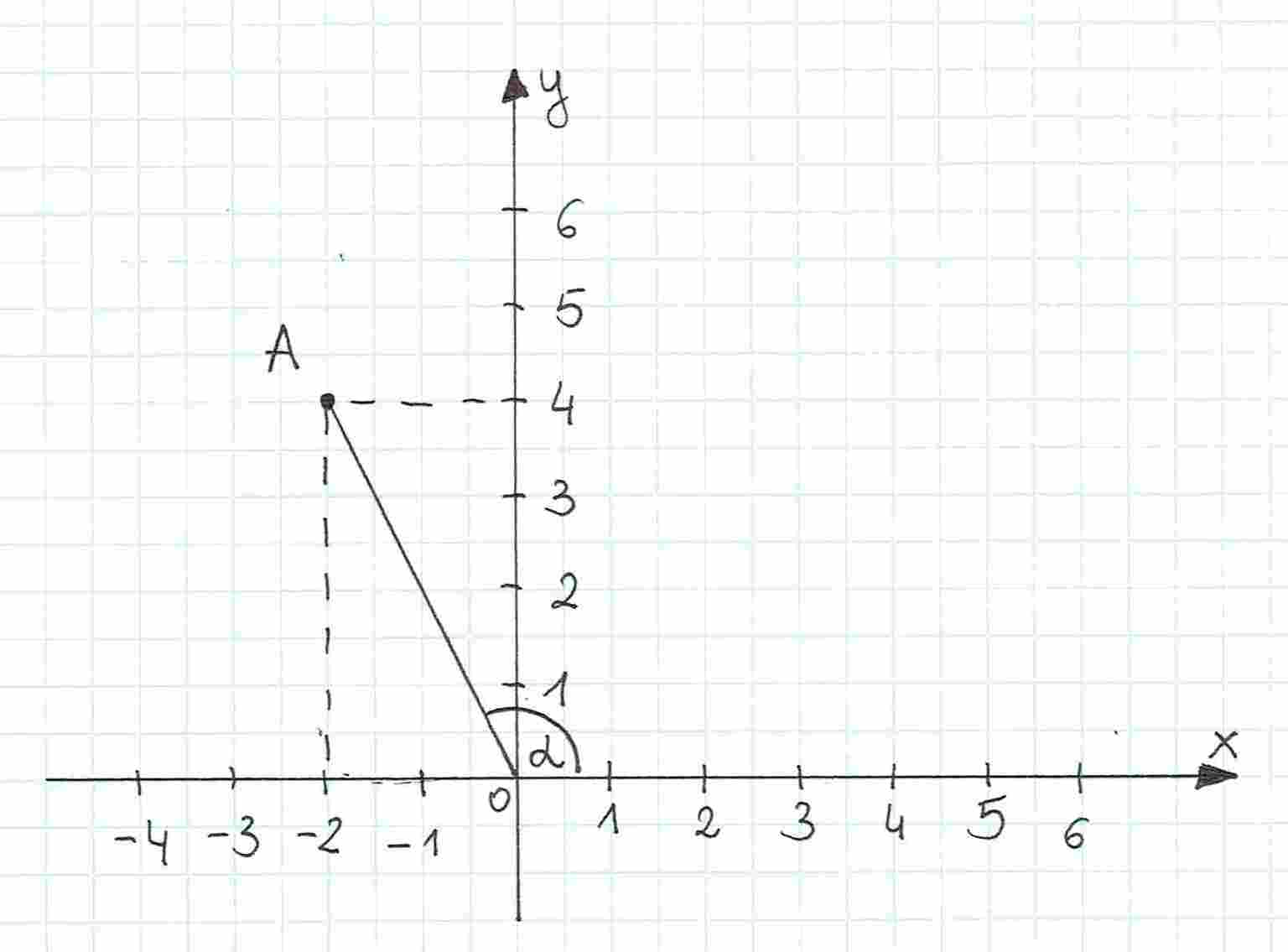
Podobnie jak poprzednio, najpierw wyznaczamy współrzędne punktu .
Teraz obliczamy długość :
Możemy wyłączyć czynnik przed pierwiastek:
Teraz możemy wyznaczyć wartości funkcji trygonometrycznych:
Jak widzisz, w obu przypadkach zasady działania są takie same, różnica jest tylko taka, że gdy kąt ma mniej niż , to sinus, cosinus i tangens są dodatnie, natomiast gdy kąt ma więcej niż (a mniej niż ), to sinus jest dodatni, a cosinus i tangens są ujemne.
Na koniec chciałabym podkreślić, że te wzory działają tylko w przypadkach, które pokazałam na rysunkach poniżej: gdy jednym z ramion jest dodatnia półoś osi (a więc wierzchołek kąta znajduje się w środku układu współrzędnych), punkt, z którego korzystamy, znajduje się na drugim ramieniu kąta, a kąt liczymy od osi przeciwnie do ruchu wskazówek zegara. Na poziomie podstawowym mogą to więc być takie przypadki:
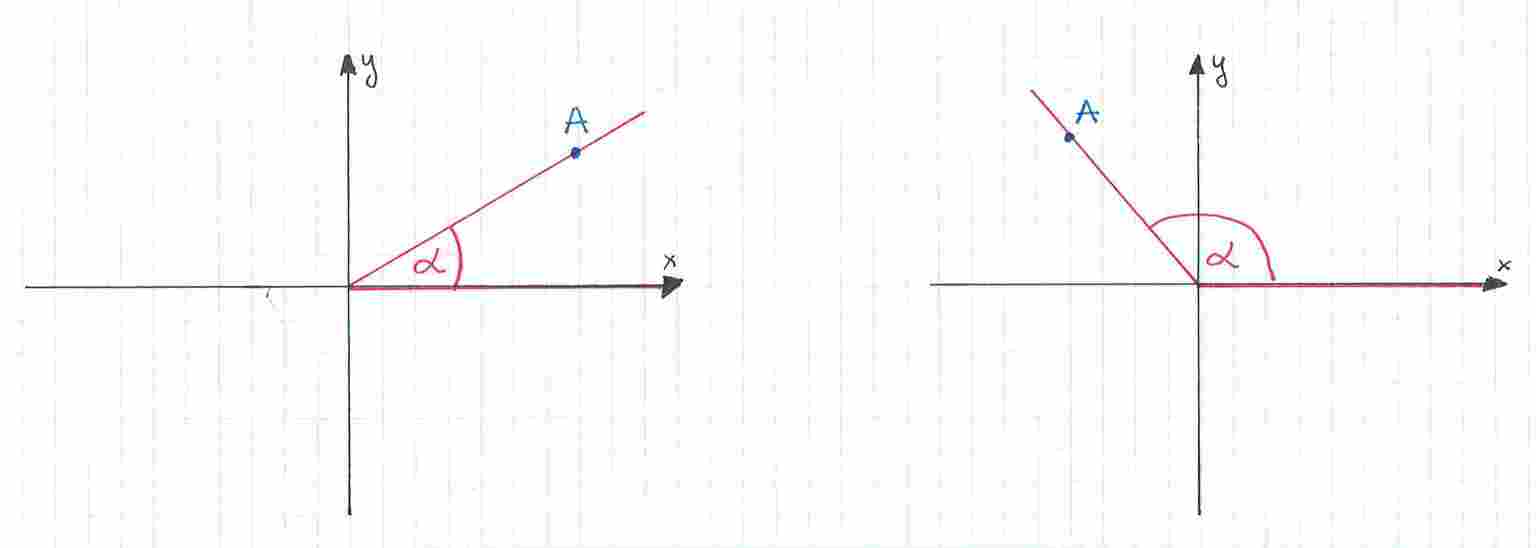
Na poziomie rozszerzonym kąty mogą być większe niż , ale wciąż muszą być spełnione te trzy warunki, byśmy mogli skorzystać z podanych wzorów. Wygląda to wtedy tak:
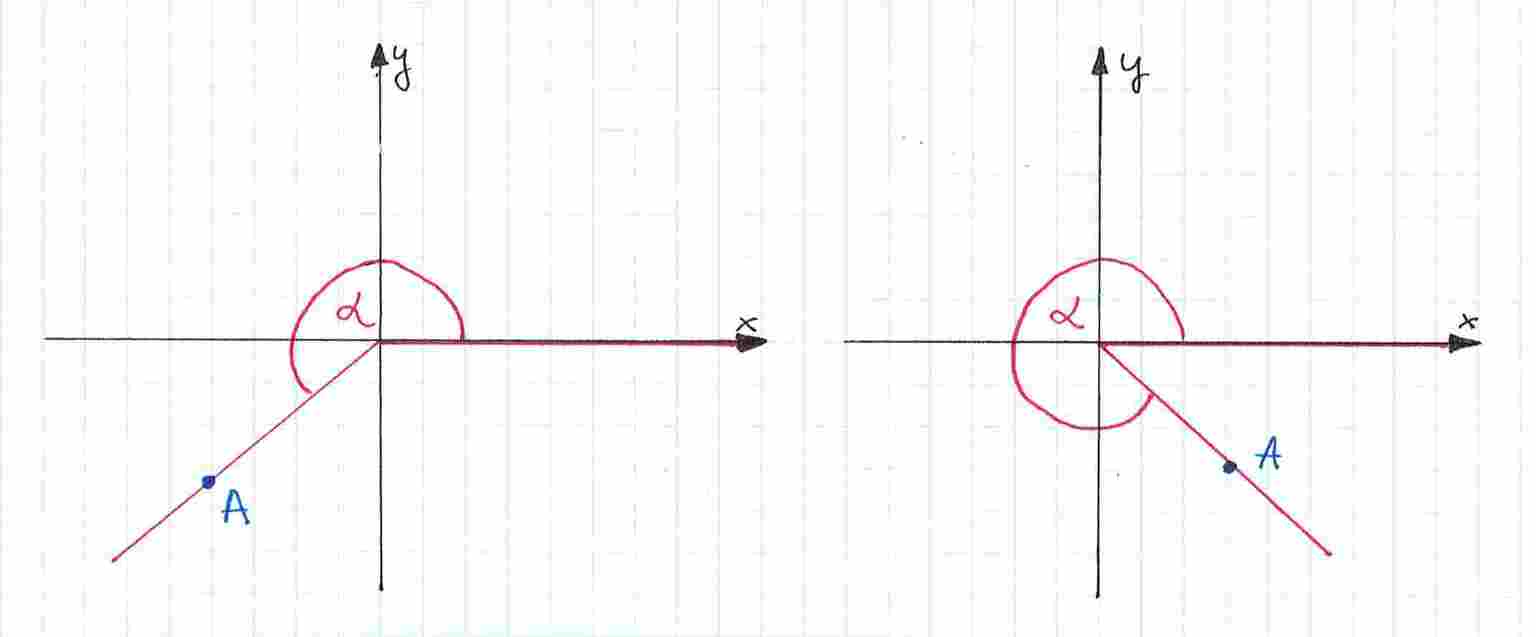
Ciekawostka: rozwartość kąta może być dowolna, a w szczególności może mieć więcej niż , tak więc osoby na poziomie rozszerzonym muszą się mierzyć również z takimi przypadkami:
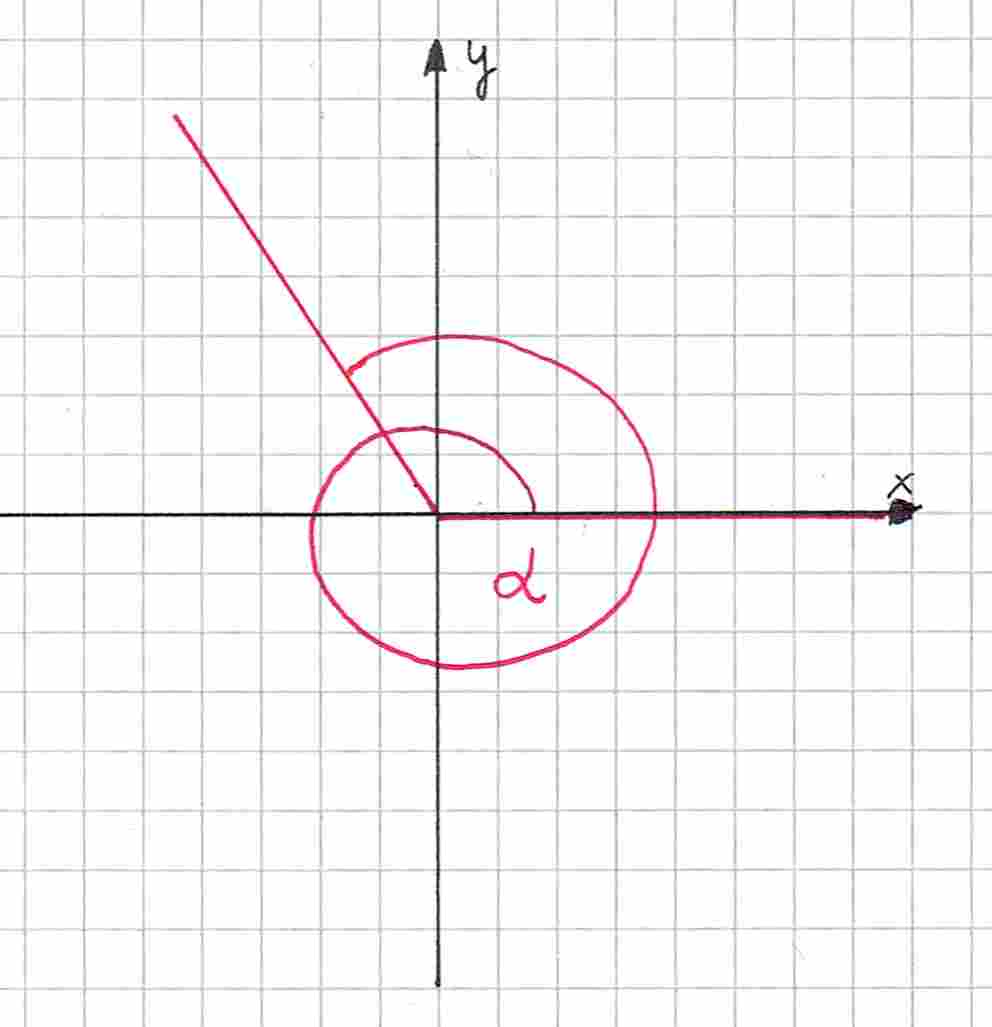
Kiedy zatem nie możemy stosować tych wzorów? Gdy nie jest spełniony któryś z trzech warunków.
Tutaj dany punkt nie znajduje się na ramieniu kąta:
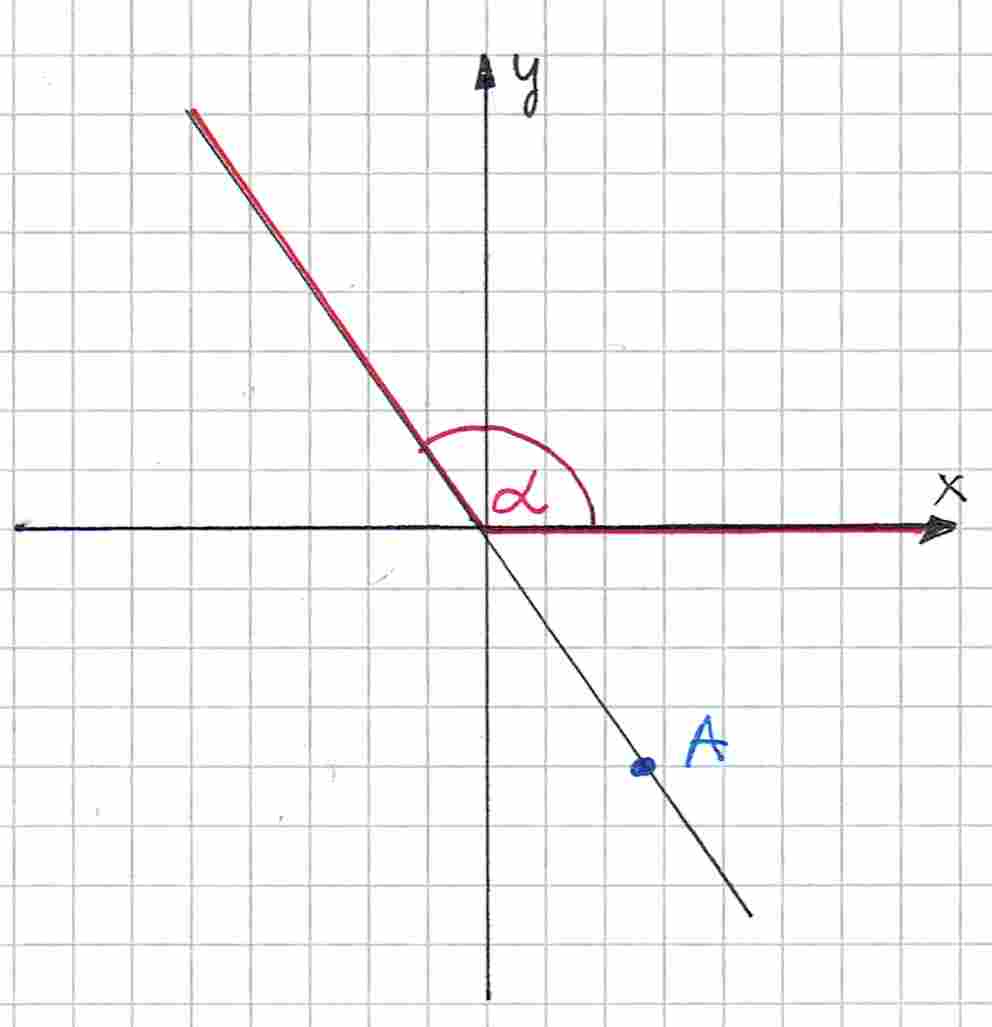
Tutaj wierzchołek kąta nie znajduje się w środku układu współrzędnych:
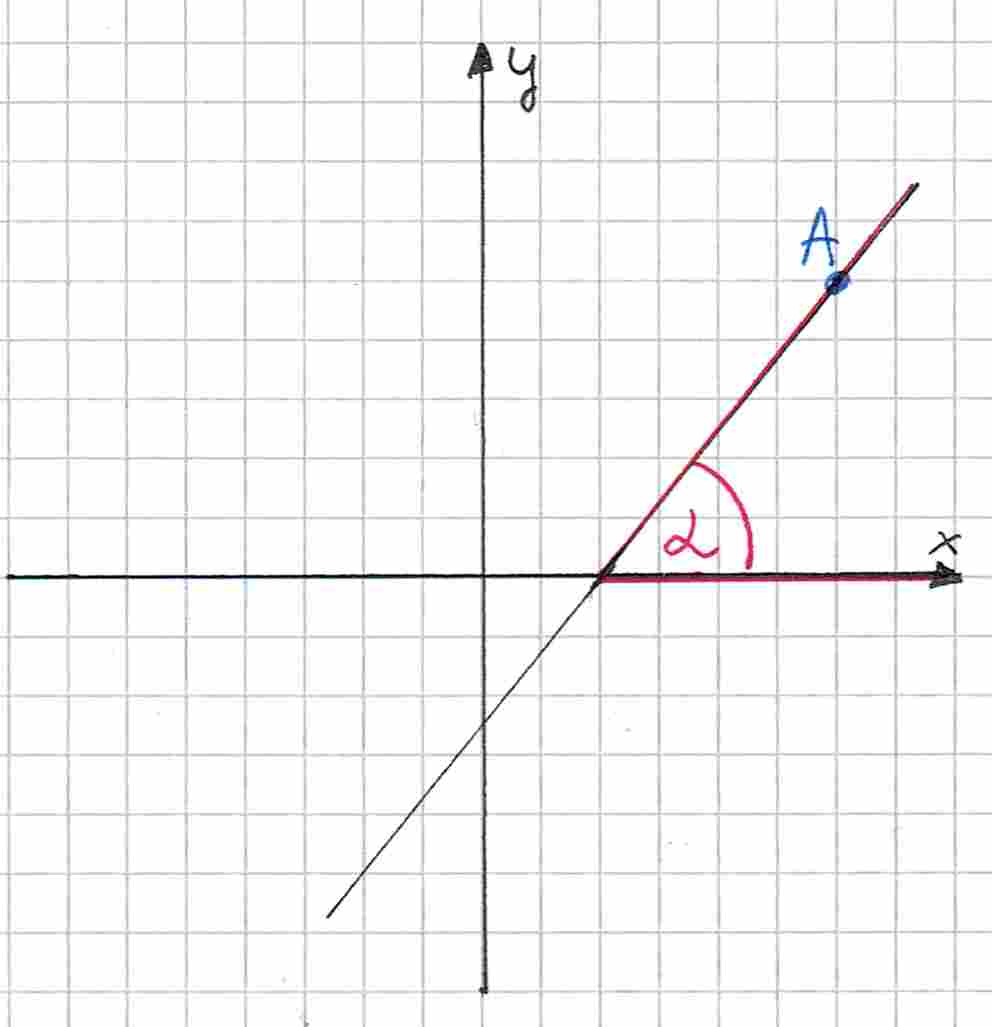
Tu natomiast kąt był liczony od osi , ale nie w tę stronę:
W pierwszych dwóch przypadkach musimy sobie poradzić geometrią analityczną, zaś w trzecim potrzebujemy wzorów z trygonometrii, ale z poziomu rozszerzonego.
Na dziś to tyle, zapraszam do części trzeciej 🙂