Z poprzednich części wiesz, jak wyznaczyć wartości funkcji trygonometrycznych, gdy masz podane boki trójkąta prostokątnego lub współrzędne punktu na płaszczyźnie. Dziś pokażę Ci, jak wyznaczyć wartości funkcji trygonometrycznych, gdy nie mamy podanej żadnej z tych rzeczy.
W takiej sytuacji polecenie może brzmieć następująco:
Jak widzisz, nie mamy tu długości boków, które moglibyśmy podstawić do wzoru na tangens. Mamy jednak wartość sinusa. Jak ją wykorzystać?
Aby sobie poradzić z takim zadaniem, musisz mieć opanowane wyznaczanie sinusa, cosinusa i tangensa w trójkącie prostokątnym. Tu możesz o tym poczytać.
Zaczynamy od narysowania trójkąta prostokątnego i zaznaczenia w nim kąta .
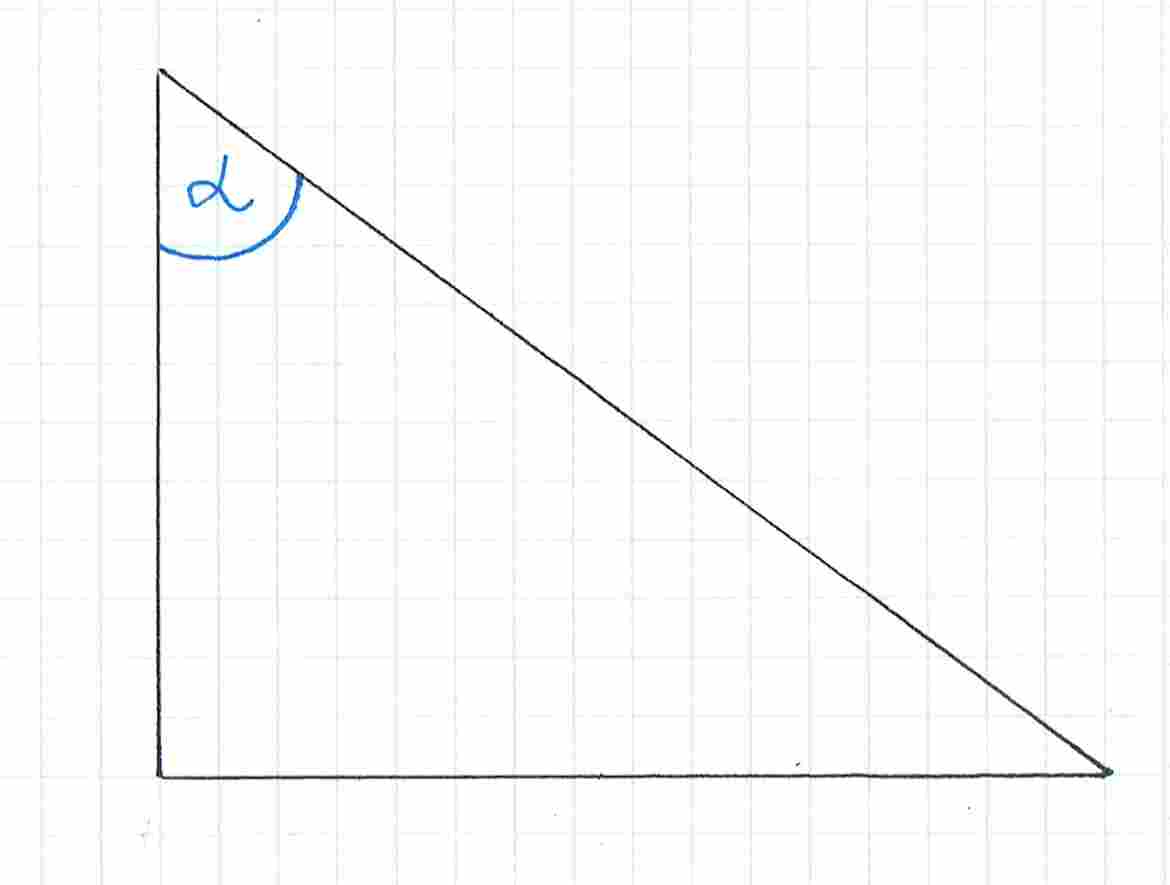
Następnie nazywamy odpowiednio boki trójkąta. Bok naprzeciwko kąta to bok , druga przyprostokątna to bok , a przeciwprostokątna to bok .
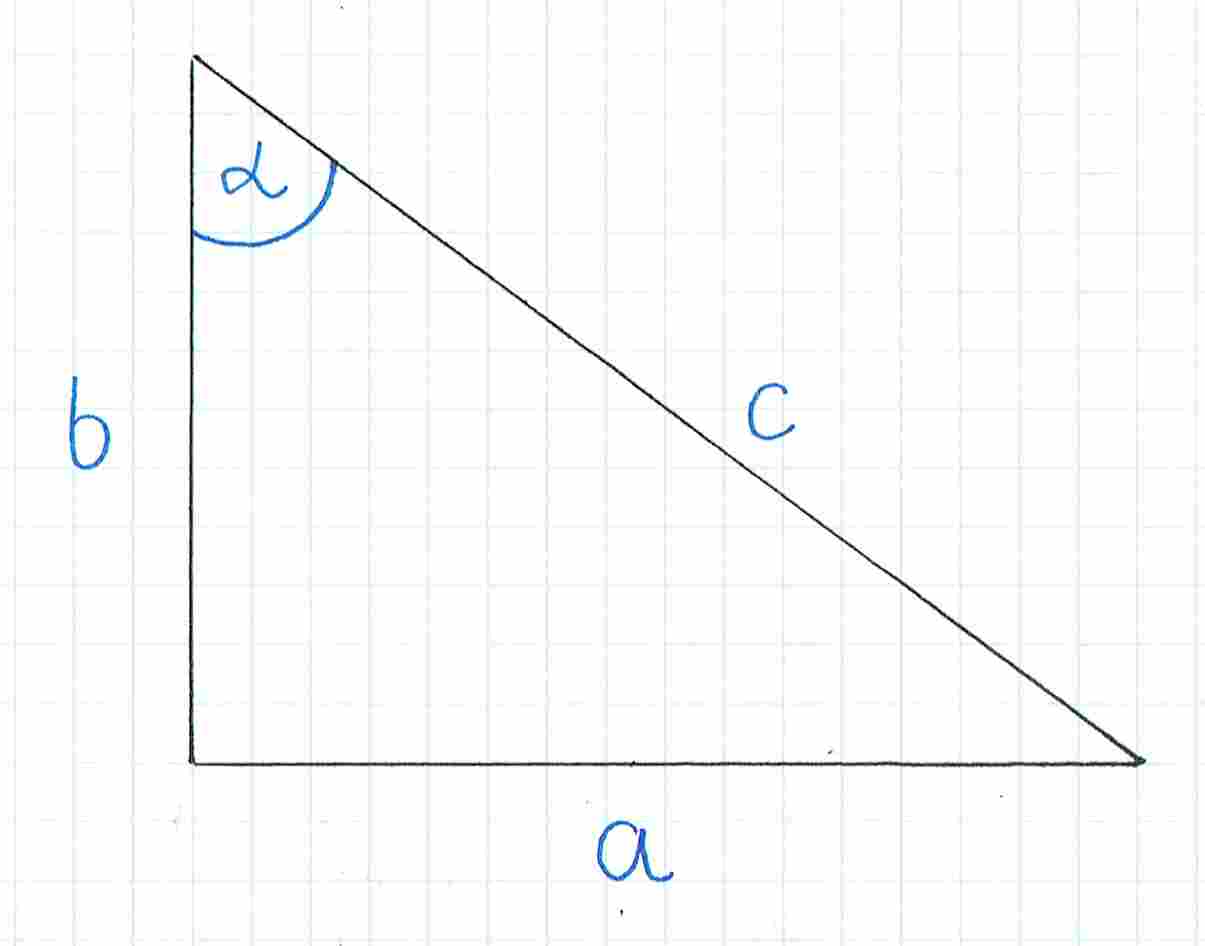
Teraz potrzebujemy wzoru na tę funkcję, którą mamy daną (czyli w naszym przypadku sinus):
Wiemy z treści zadania, że , stąd
Możemy więc przyjąć, że , a , gdzie może być dowolną dodatnią liczbą. (Pod rozwiązaniem tego zadania bardziej szczegółowo tłumaczę, dlaczego tak i o co chodzi z tym -em, póki co przyjmijmy, że faktycznie tak jest.)
Zaznaczamy otrzymane wartości na rysunku:
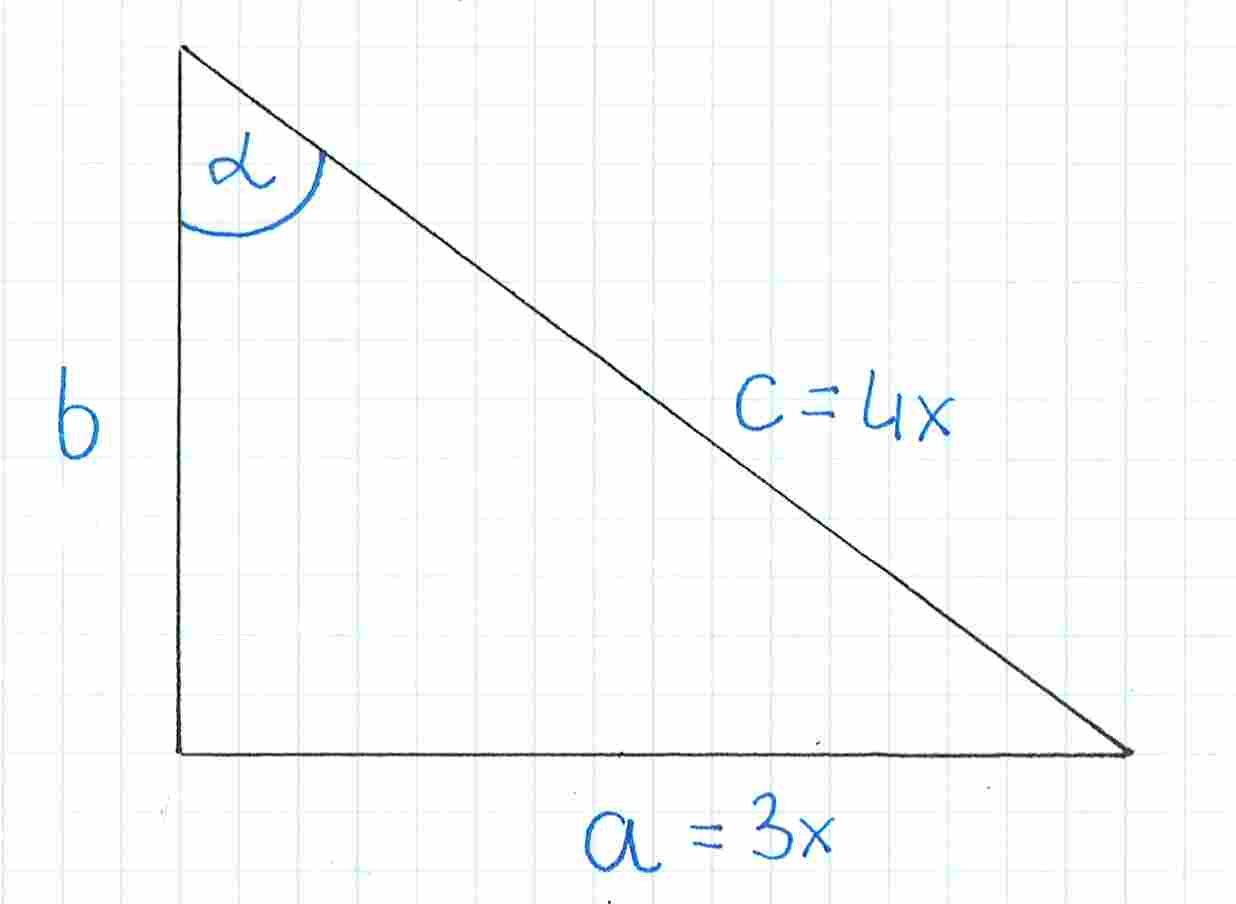
Teraz, gdy mamy dwa boki trójkąta, możemy wyznaczyć trzeci przy pomocy twierdzenia Pitagorasa:
Możemy otrzymany wynik zaznaczyć na rysunku:
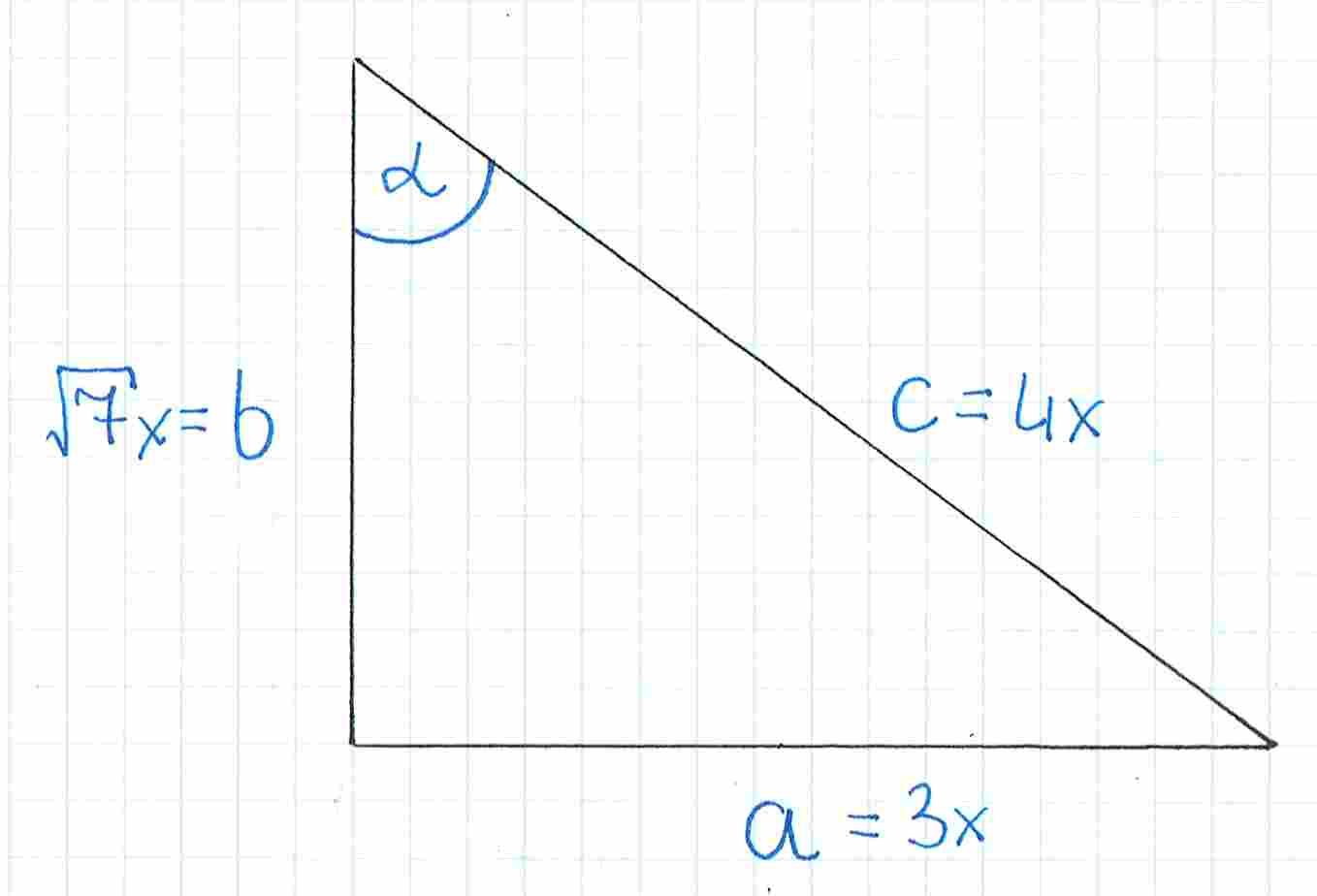
Teraz mamy już wszystko, by obliczyć wartość tangensa, o którą proszą w zadaniu. Potrzebujemy tylko wzoru:
Dla porządku możemy jeszcze usunąć niewymierność z mianownika:
_________________________________________________
No dobra, to o co chodzi z tym -em?
Wróćmy do początku. Mamy taki trójkąt:
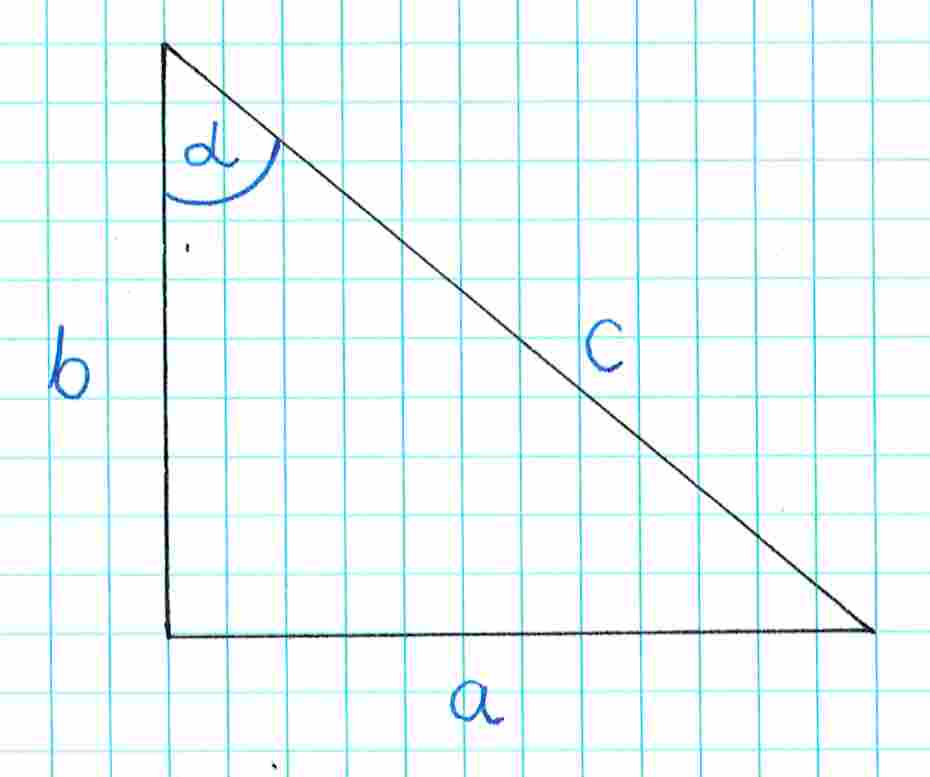
Wiemy, że . Dlaczego nie możemy więc po prostu napisać, że i ? Tak w zasadzie to możemy. Taki trójkąt spełnia warunki zadania i uzyskamy dla niego poprawny wynik.
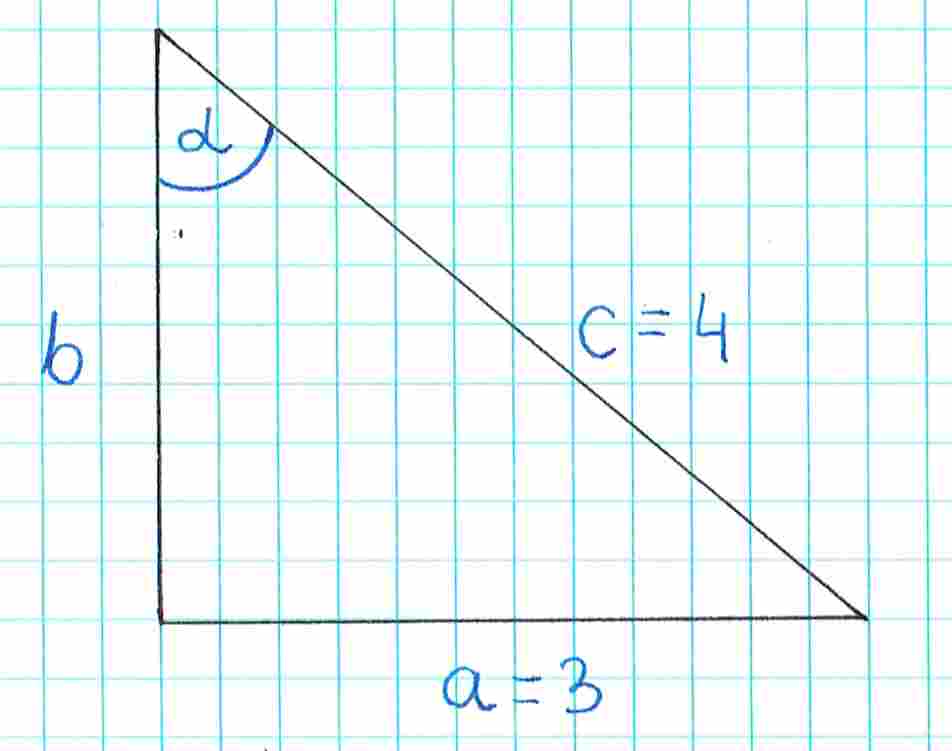
Musimy jednak mieć świadomość, że jest to jeden z nieskończenie wielu trójkątów, które spełniają warunki zadania.
Popatrz na ten trójkąt:
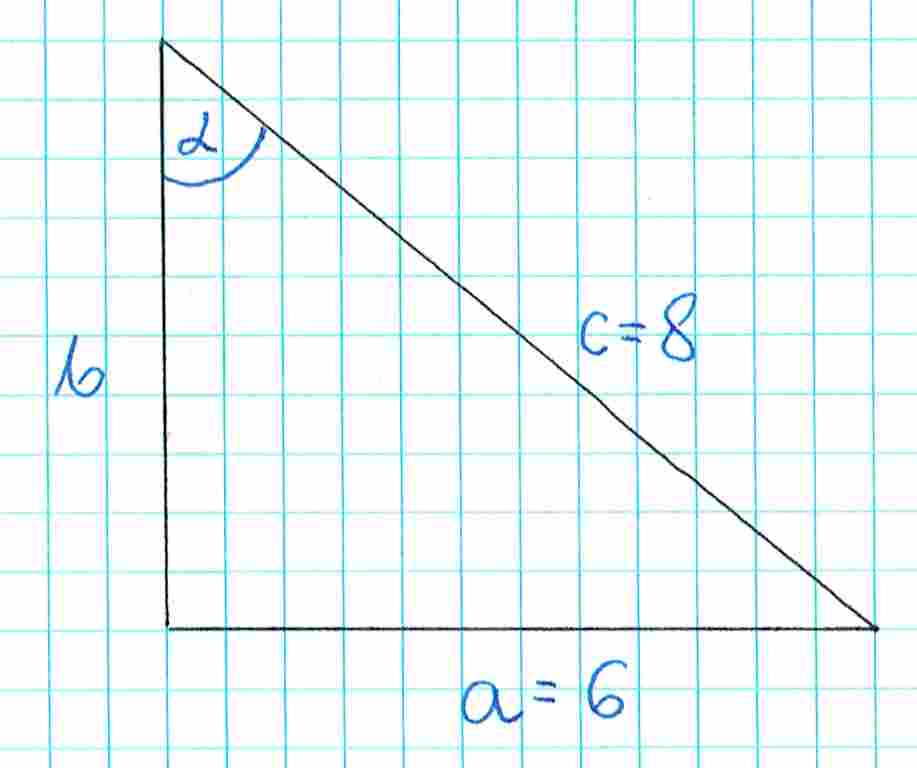
Jeśli policzymy sinus kąta , to zobacz, co otrzymamy:
Dla innego trójkąta otrzymaliśmy taki sam wynik sinusa. Dzieje się tak dlatego, że funkcje trygonometryczne tak naprawdę nie operują długościami boków, a jedynie proporcjami między nimi. Dlatego zapisując zamiast , uwzględniamy, że to mogą być różne trójkąty. Moim zdaniem jest to ważne, bo o ile w tym zadaniu i tak otrzymamy poprawny wynik, o tyle są takie zadania, gdzie to ma znaczenie. Jeśli z matematyką radzisz sobie kiepsko, to jest duża szansa, że nie wychwycisz, że akurat w tym zadaniu trzeba wstawić tego -a, dlatego bezpieczniej jest go wstawiać zawsze.
__________________________________________________
Teraz inny przykład:
Działamy tak samo, jak poprzednio. Najpierw rysujemy trójkąt prostokątny i zaznaczamy w nim kąt , a następnie nazywamy odpowiednio boki:

Teraz potrzebujemy wzoru na tę funkcję, której wartość mamy podaną, czyli cosinus:
Wiemy, że , stąd
Możemy stąd wywnioskować, że (czyli po prostu ), a . Zaznaczamy to na rysunku:
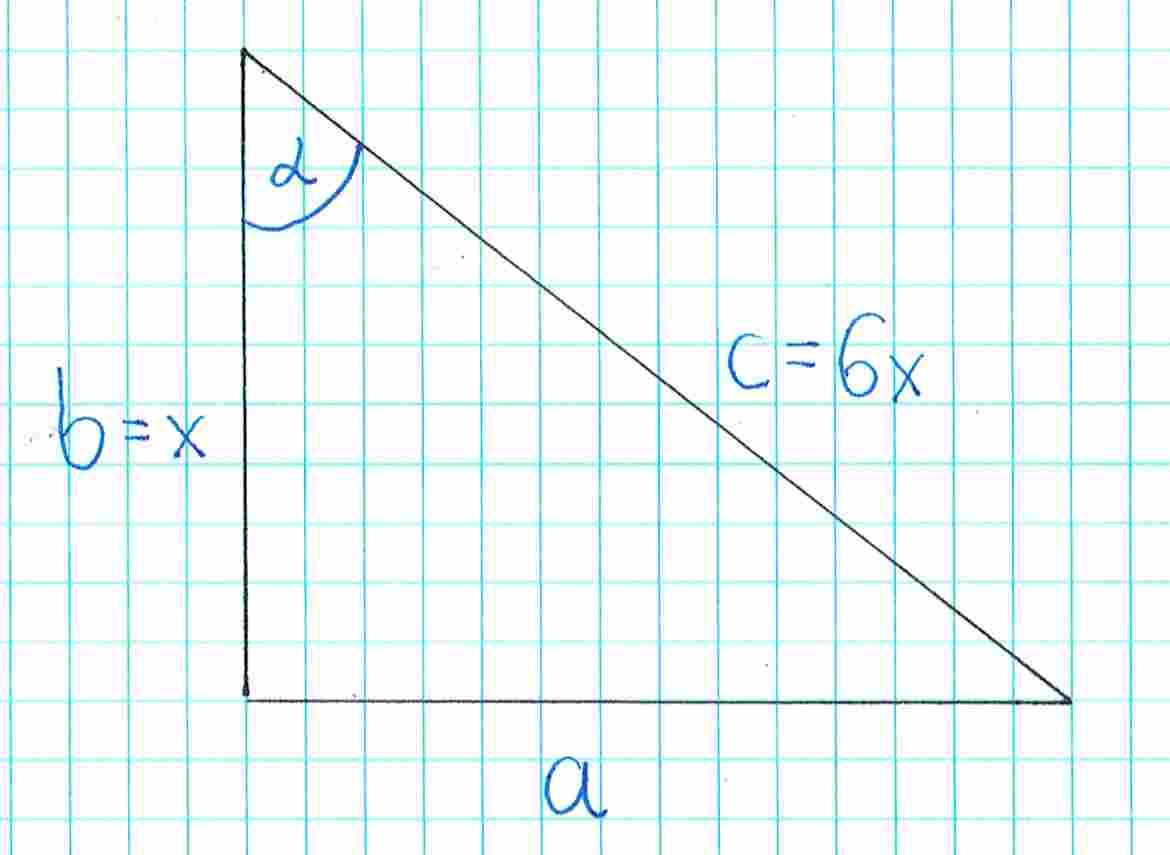
Aby wyznaczyć sinus, potrzebujemy długość boku . Wyznaczymy ją z twierdzenia Pitagorasa:
Możemy otrzymaną długość zaznaczyć na rysunku:
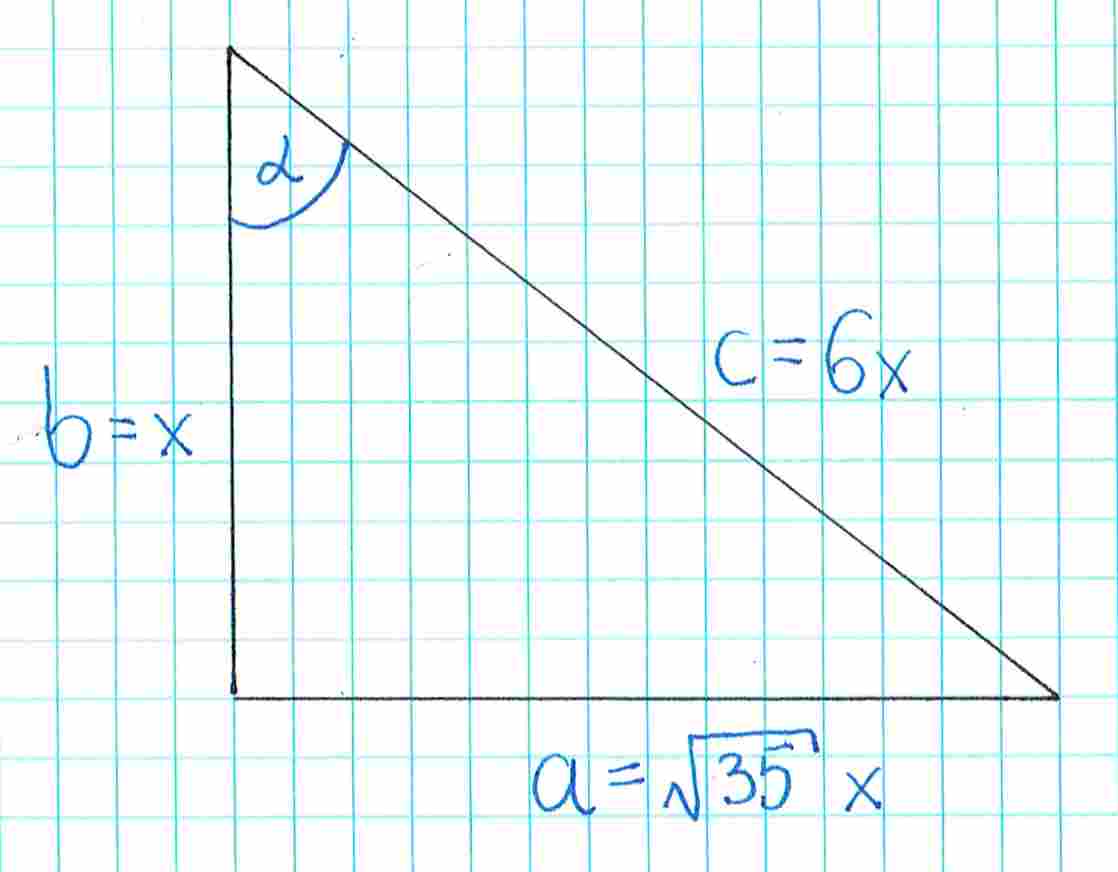
Teraz możemy już wyznaczyć wartość sinusa. Potrzebujemy wzoru:
______________________________________________
Myślę, że już ogarniasz, jak się rozwiązuje takie zadania, więc teraz dwa przykłady, które mogą być nieco podchwytliwe.
Rysujemy trójkąt:

Zapiszmy wzór funkcji, której wartość mamy podaną (czyli wzór na tangens):
Wiemy, że , stąd
Sprawa się komplikuje, bo wartość naszego tangensa nie jest ułamkiem. W takim wypadku należy sobie taki ułamek stworzyć: to inaczej :
Oznaczamy, że i :
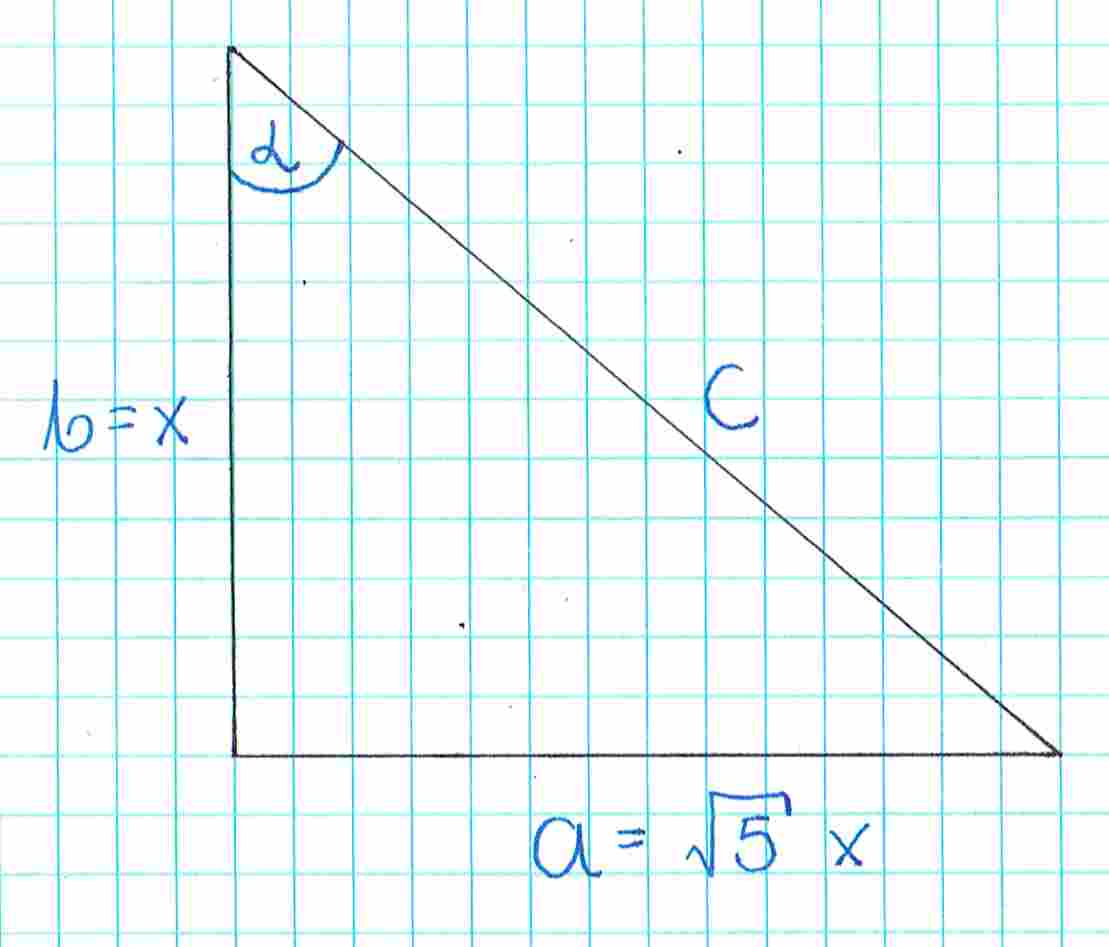
Bok wyznaczamy z twierdzenia Pitagorasa:
Zaznaczamy na rysunku bok :
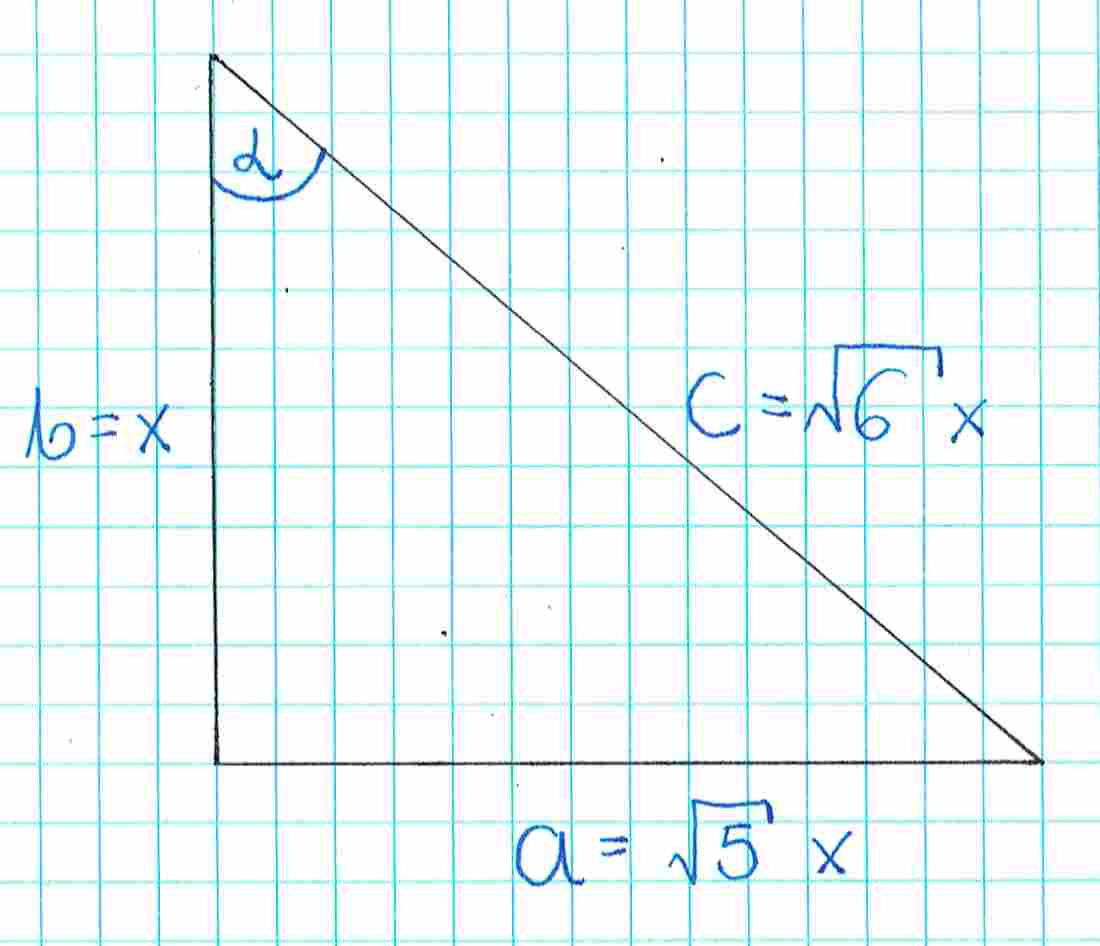
Teraz potrzebujemy wzoru funkcji, której wartość chcemy obliczyć, czyli cosinusa:
Podstawiamy:
______________________________________________
Być może zastanawiasz się, po co w treści zadania umieszczony jest zapis, że kąt jest ostry. Jest on po to, byśmy wiedzieli, że wszystkie wartości funkcji są dodatnie. Dla kątów, które nie są ostre, mogłyby się nam przypałętać minusy, które nieco komplikują sprawę.
______________________________________________
Na koniec zadanie, w którym trzeba się pilnować, by się nie pogubić:
Jak pewnie zwróciłeś uwagę, kąty są dwa. Musimy więc pilnować, dla którego kąta co wyznaczamy.
Zaczynamy od narysowania trójkąta i zaznaczenia w nim kątów.
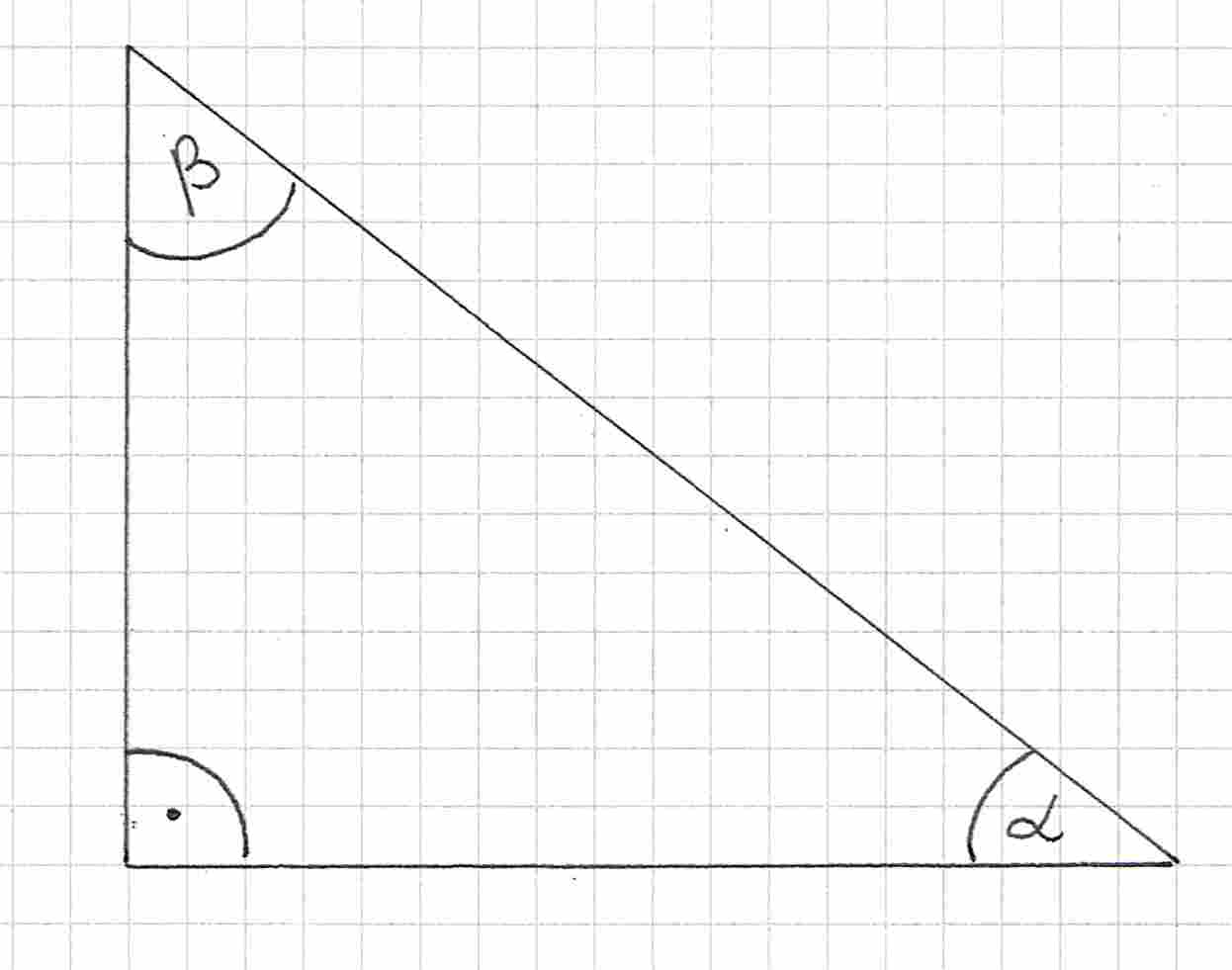
Następnie musimy nazwać odpowiednio boki. Jak zawsze zaczynamy od wykorzystania tej funkcji, którą mamy daną. My znamy , więc będziemy oznaczać boki względem kąta .
Bok naprzeciwko kąta to bok , druga przyprostokątna to bok , a przeciwprostokątna to bok .
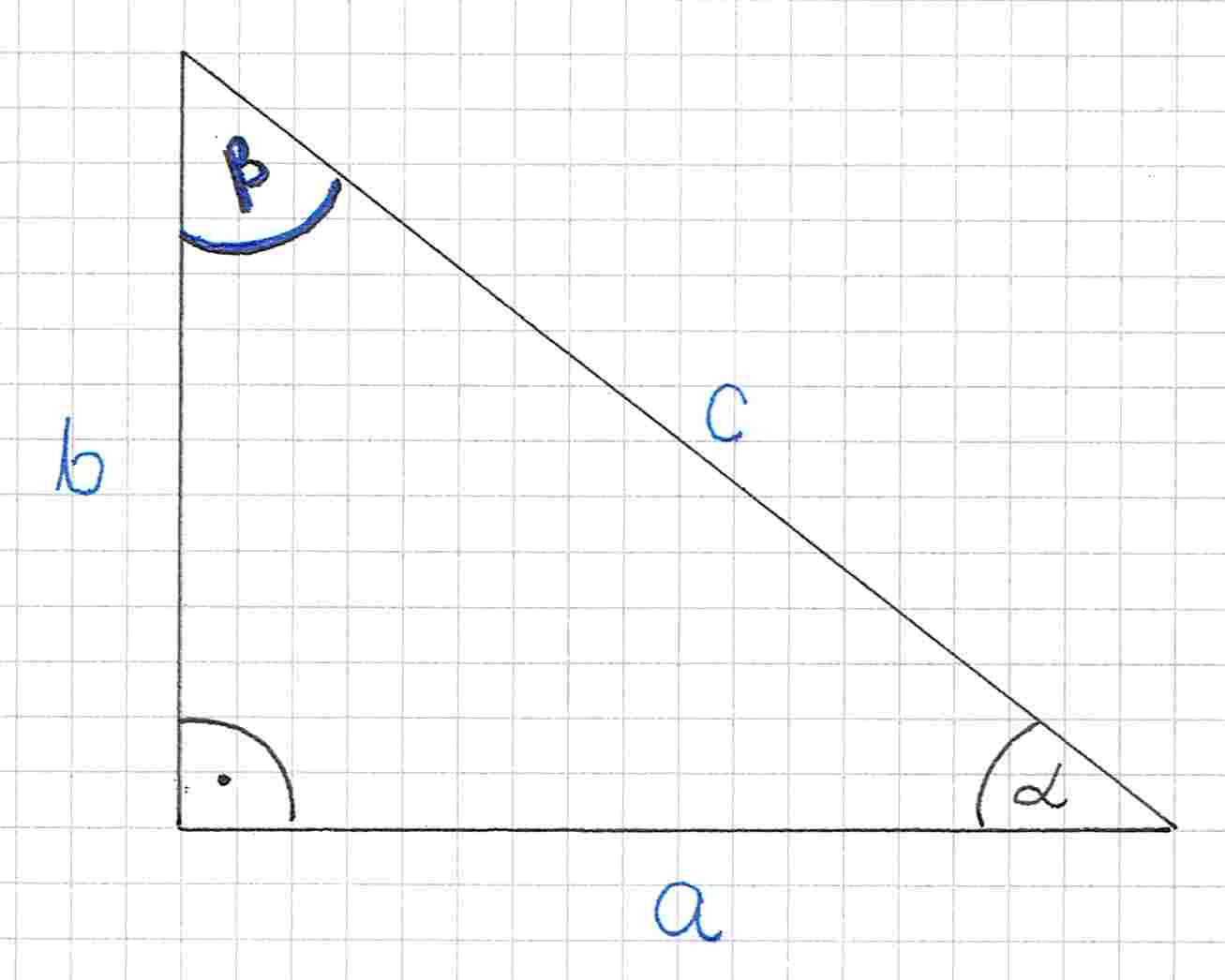
Wiemy, że . Potrzebujemy teraz wzoru na tangens:
Skoro , to możemy zapisać, że , a :
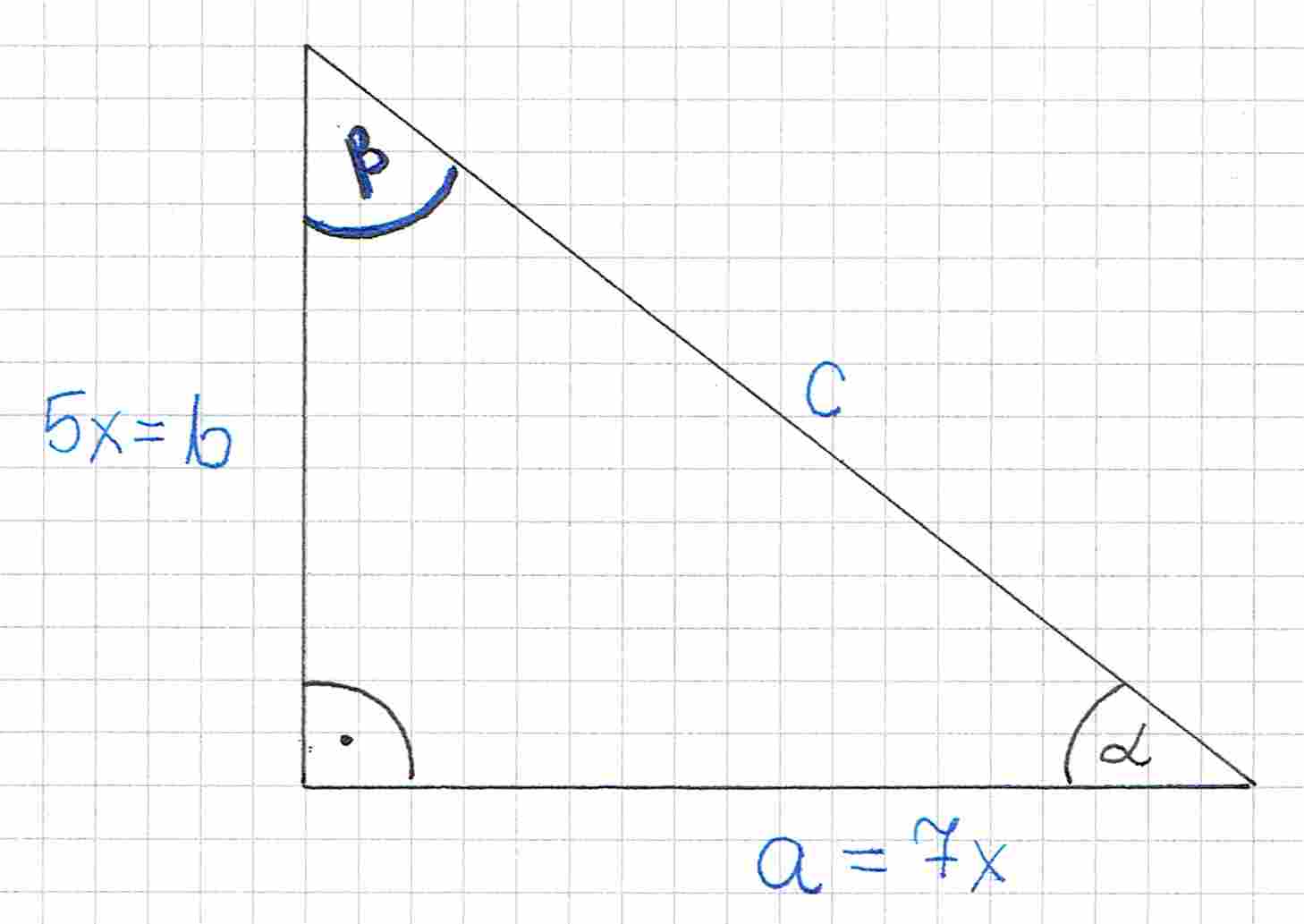
Do wyznaczenia cosinusa potrzebujemy długość boku . Wyznaczamy ją z twierdzenia Pitagorasa:
Nanosimy wynik na rysunek:
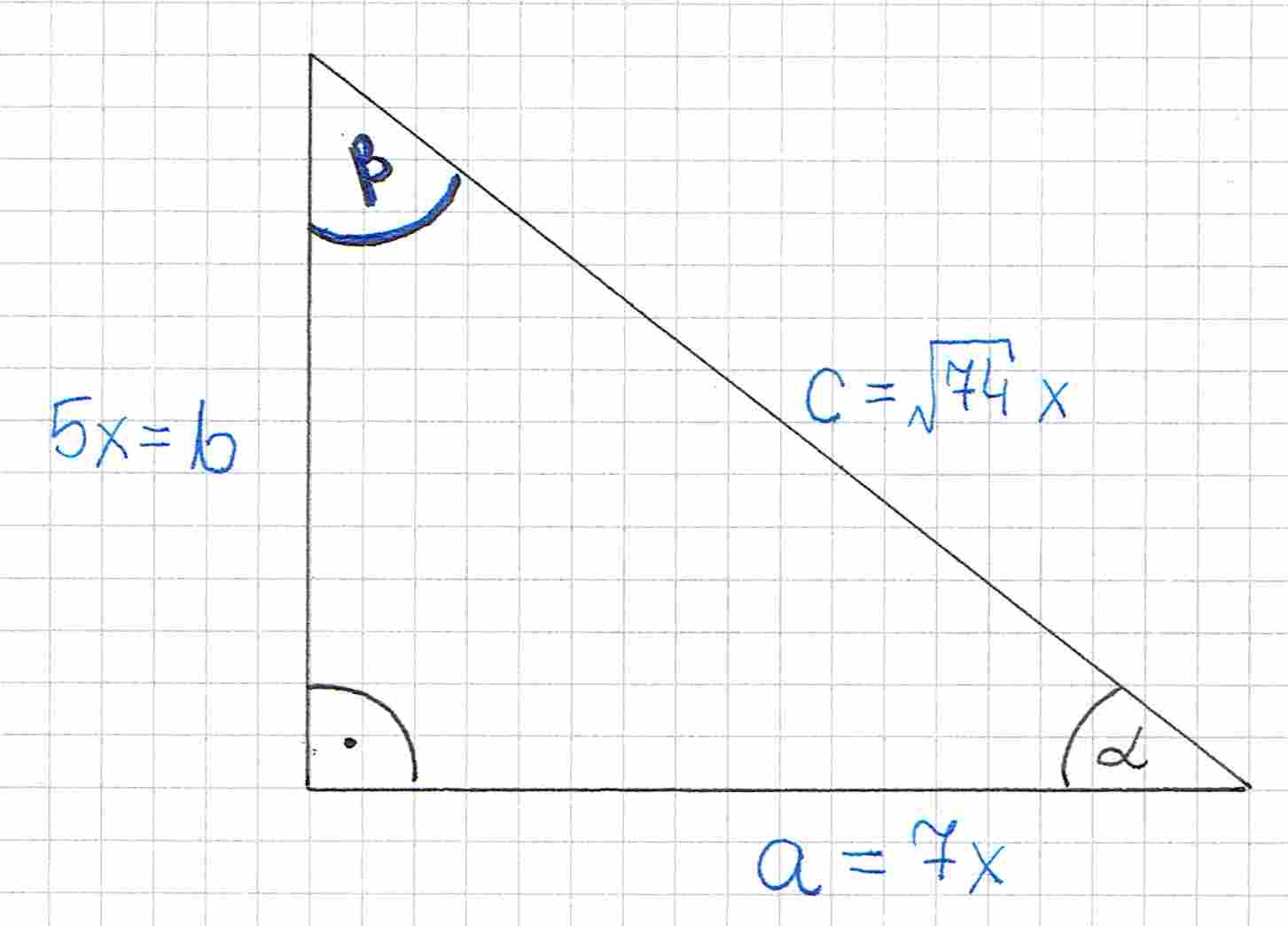
Teraz możemy już wyznaczyć cosinusa. No, prawie. Pamiętaj, że mamy wyznaczyć - musimy więc od nowa ponazywać boki, tym razem względem kąta !
Bok naprzeciwko kąta to bok , druga przyprostokątna to bok , a przeciwprostokątna to bok (ona zostaje bez zmian).
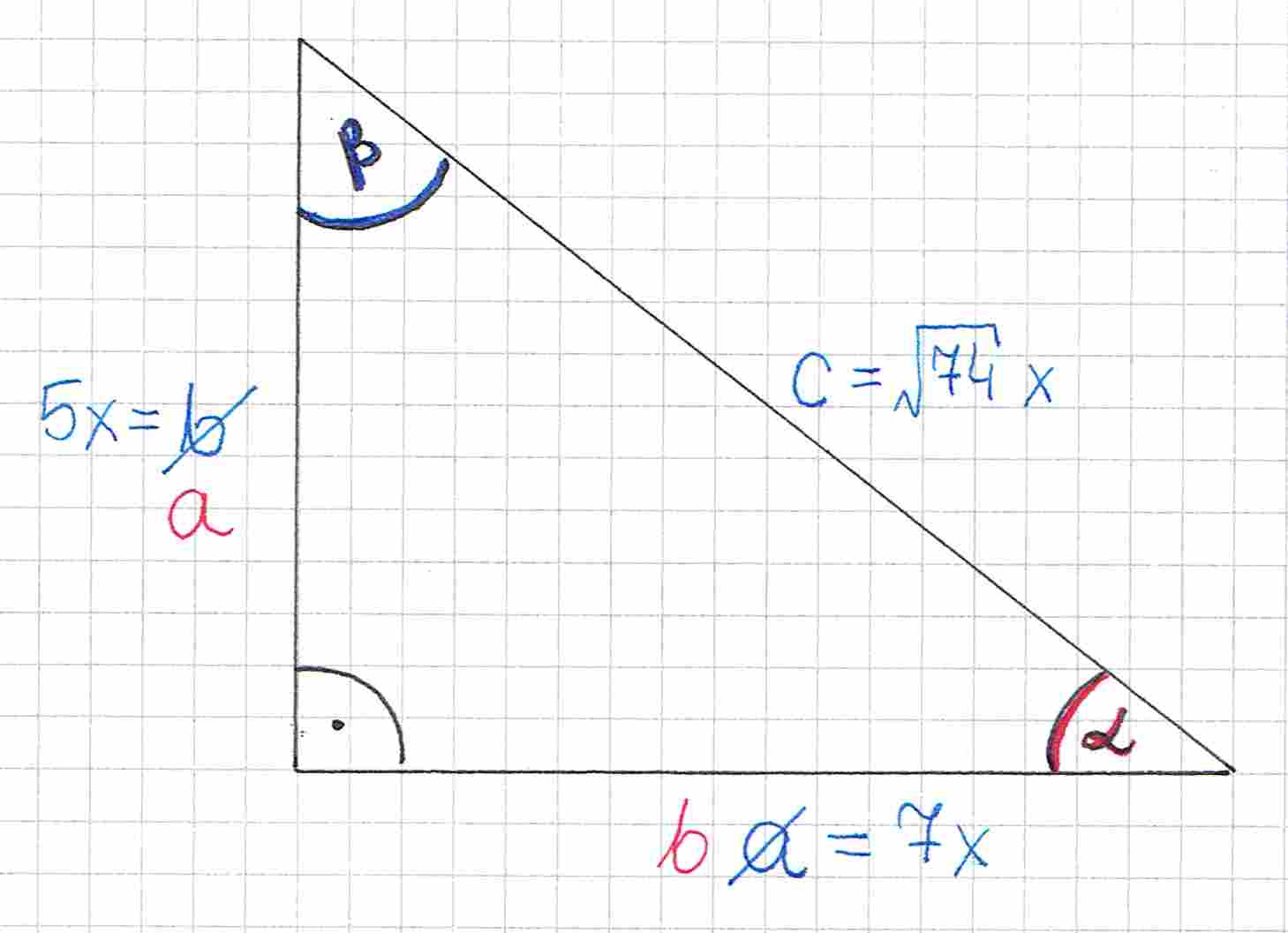
Potrzebujemy wzoru na cosinusa:
_______________________________________________
Na dziś to tyle 🙂