Cześć! Witam Cię w wyzwaniu maturalnym, czyli w trwającej dwa miesiące wspólnej powtórce do matury podstawowej z matematyki. Będziemy razem rozwiązywać zadania, wdrażać techniki efektywnego uczenia się, oswajać się z tablicami matematycznymi, tworzyć własną kartę ze wzorami, których nie ma w tablicach, dowiesz się też, jak wykorzystać klucz maturalny na swoją korzyść 🙂
Codziennie dostaniesz ode mnie zadania do wykonania. W dniach od poniedziałku do soboty będą to trzy zadania, w niedzielę jedno lub dwa. Zazwyczaj będą to po prostu zadania maturalne, ale czasem (w niedziele, ale okazyjnie też w inne dni) będą to zadania polegające na obejrzeniu czegoś, zastanowieniu się nad czymś czy na wdrożeniu jakiejś techniki.
Najważniejsza zasada: zadania musisz rozwiązywać - czytanie czy oglądanie rozwiązań zdecydowanie nie wystarczy!
Na początku spróbuj rozwiązać zadanie samodzielnie. Nawet jeśli nie masz pojęcia, o co w nim chodzi, spróbuj - może w tablicach maturalnych znajdziesz informacje, które Ci pomogą?
Jeśli zadanie zostało przez Ciebie rozwiązane samodzielnie, możesz je uznać za zaliczone 🙂 Jeśli natomiast nie udało Ci się rozwiązać zadania, przeczytaj lub obejrzyj rozwiązanie. Wróć do zadania po przerwie (na przykład godzinnej) i spróbuj je rozwiązać bez patrzenia na rozwiązanie. Jeśli się udało - zaliczone 🙂 Jeśli nie, spróbuj następnego dnia 🙂
Jeśli jakieś zadanie sprawia Ci dużą trudność, skorzystaj z materiałów, które są pod nim podlinkowane - tam zagadnienie będzie wytłumaczone dużo bardziej szczegółowo.
To, że nie umiesz zrobić jakiegoś zadania nie oznacza, że nie możesz przejść do następnych - jak najbardziej możesz 🙂 Ale pamiętaj, by regularnie wracać do tego niezrobionego - jeśli materiały ode mnie nie są dla Ciebie wystarczające, może poproś kogoś, by Ci je wytłumaczył?
Jeśli mimo wielu prób, przerobienia dodatkowych materiałów i skorzystania z pomocy innych osób nie możesz uporać się z jakimś zadaniem, odpuść je - żeby zdać maturę, nie musisz przecież napisać na 100%. Ważne, by takich zadań nie było zbyt dużo.
Wybrane wzory matematyczne - czyli karta wzorów, którą dostaniesz na maturze
Wybrane wzory matematyczne 2.0 - czyli karta wzorów z zaznaczonymi przeze mnie wzorami, które obowiązują Cię na poziomie podstawowym
UWAGA: jeśli po pobraniu kart nie widzisz pozakreślanych wzorów, tylko zwykłe tablice, pobierz ten plik - zajmuje więcej miejsca, ale na pewno będzie działał
W materiałach do pobrania znajdziesz wzory, których nie ma w tablicach matematycznych, kóre dostaniesz na maturze. Pobierz je, przejrzyj i zdecyduj, czego chciałbyś/chciałabyś się nauczyć, a co uznajesz za niepotrzebne 🙂
Zadanie 1
Prosta jest styczna w punkcie do okręgu o środku . Punkt leży na tym okręgu i miara kąta jest równa . Przez punkty i poprowadzono prostą, która przecina prostą w punkcie (zobacz rysunek).

A.
B.
C.
D.
Zadanie 2
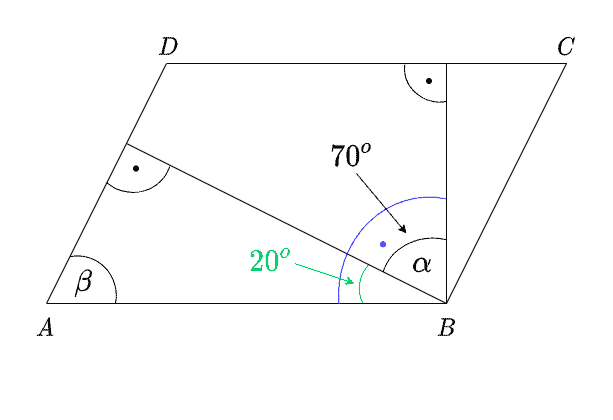
W równoległoboku , przedstawionym na rysunku, kąt ma miarę .

A.
B.
C.
D.
Zadanie 3
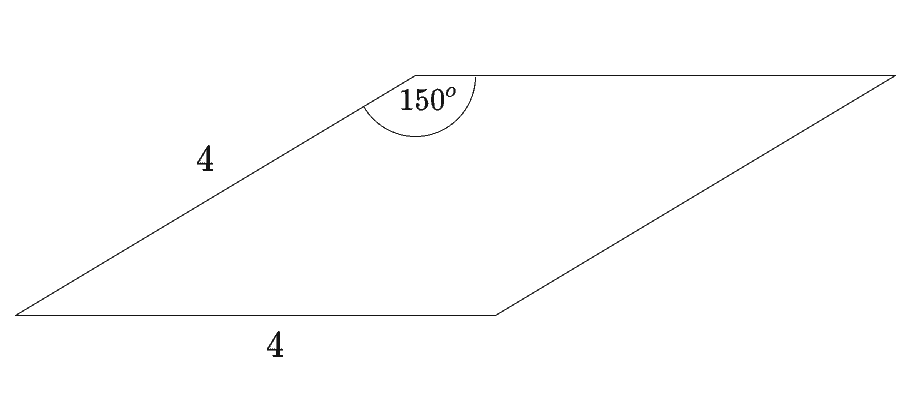
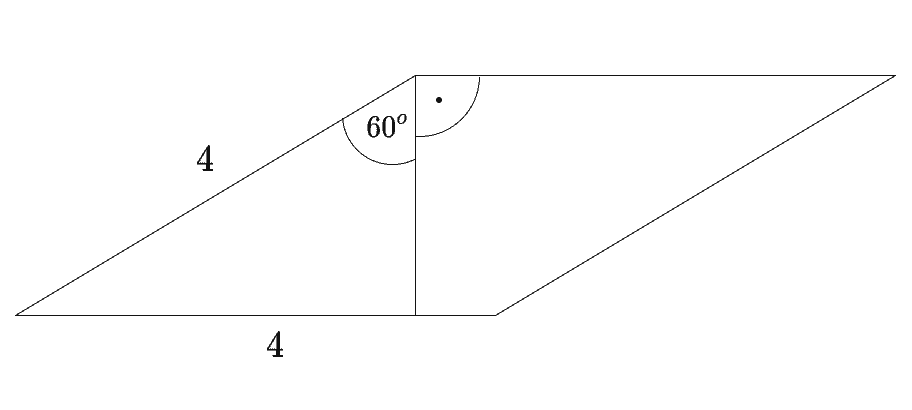
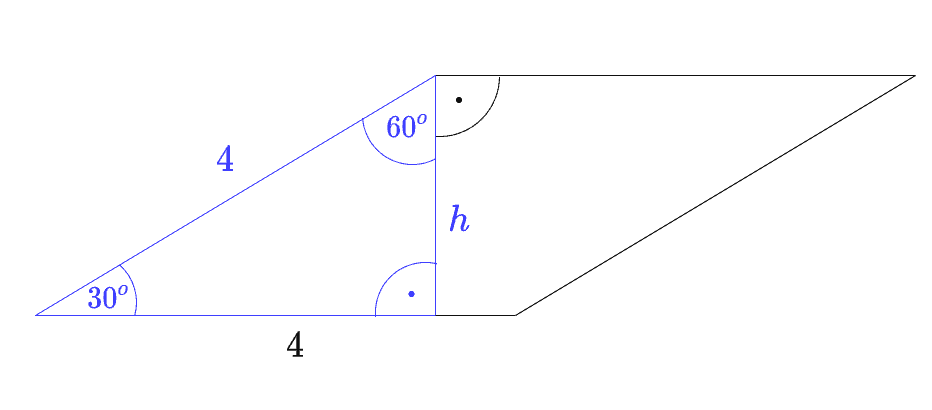
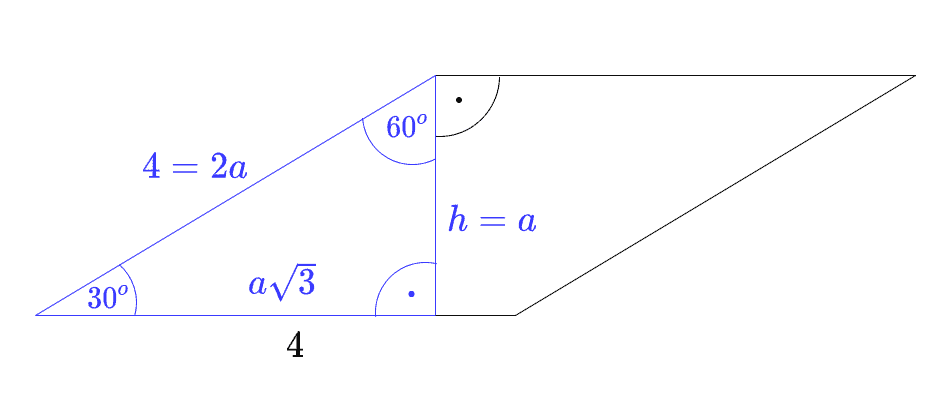
Dany jest romb o boku długości i kącie rozwartym . Pole tego rombu jest równe
A.
B.
C.
D.
Materiały dodatkowe 1
Materiały dodatkowe 2
Zadanie 1
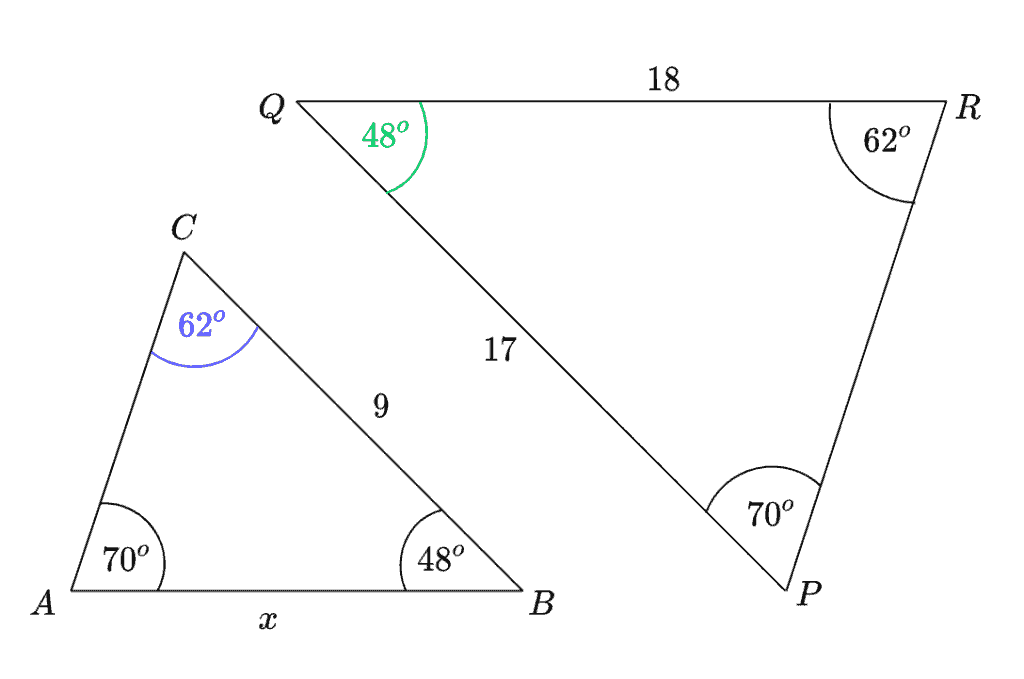
Przedstawione na rysunku trójkąty i są podobne. Bok trójkąta ma długość

A.
B.
C.
D.
Zadanie 2
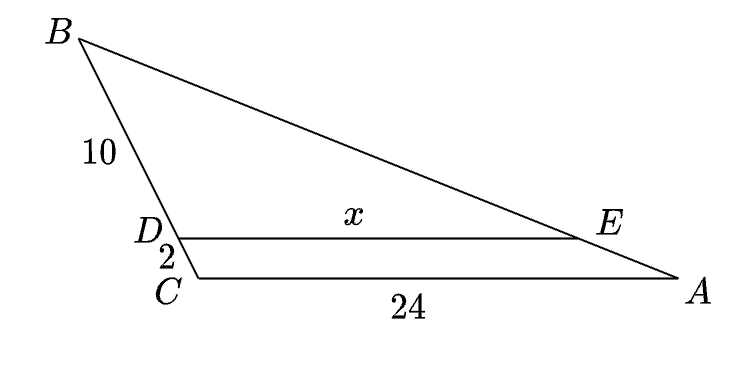
W trójkącie punkt leży na boku , a punkt leży na boku . Odcinek jest równoległy do boku , a ponadto , i (zobacz rysunek).

A.
B.
C.
D.
Zadanie 3
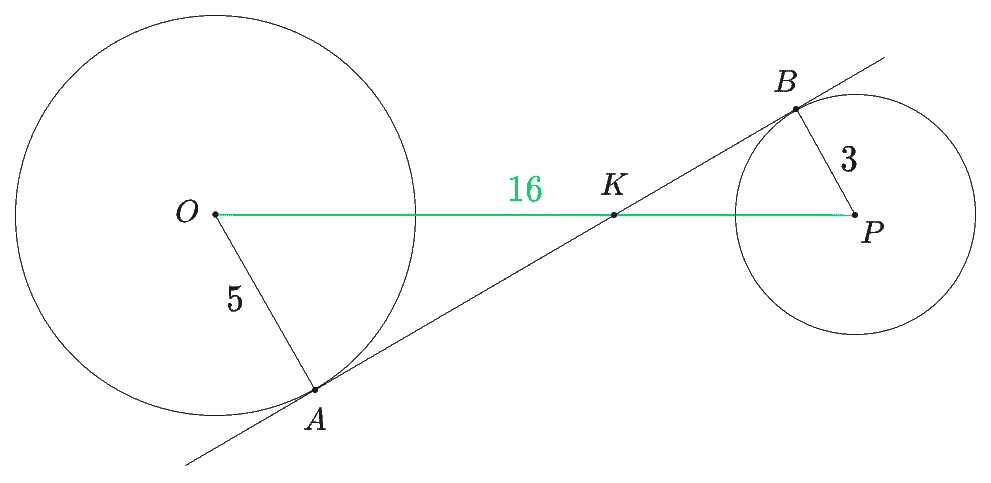
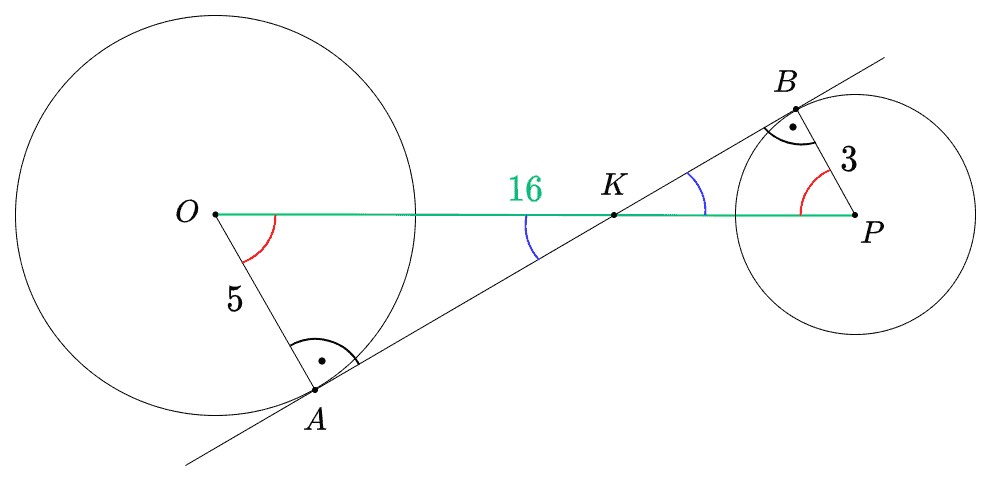
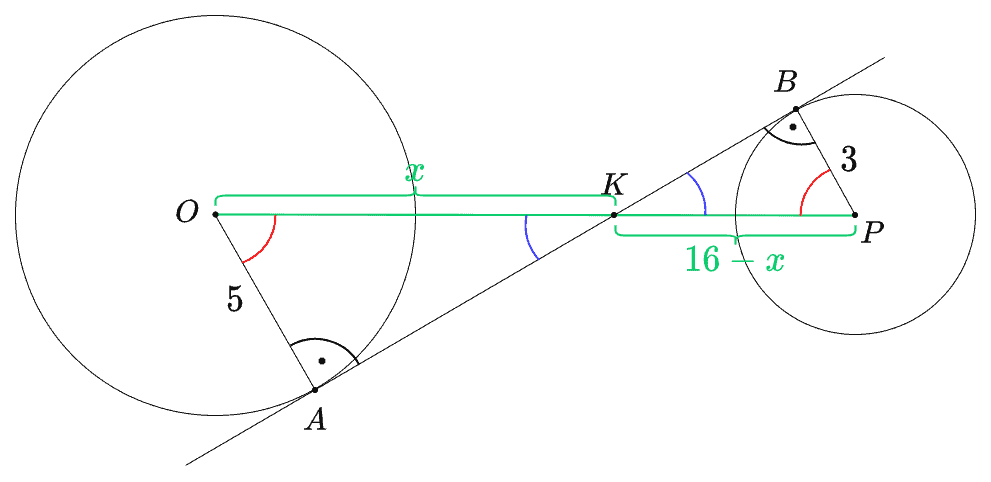
Dane są dwa okręgi: okrąg o środku w punkcie i promieniu oraz okrąg o środku w punkcie i promieniu . Odcinek ma długość . Prosta jest styczna do tych okręgów w punktach i . Ponadto prosta przecina odcinek w punkcie (zobacz rysunek).

A.
B.
C.
D.
Materiały dodatkowe
Zadanie 1
Wykresem funkcji kwadratowej jest parabola, której wierzchołkiem jest punkt o współrzędnych
A.
B.
C.
D.
Zadanie 2
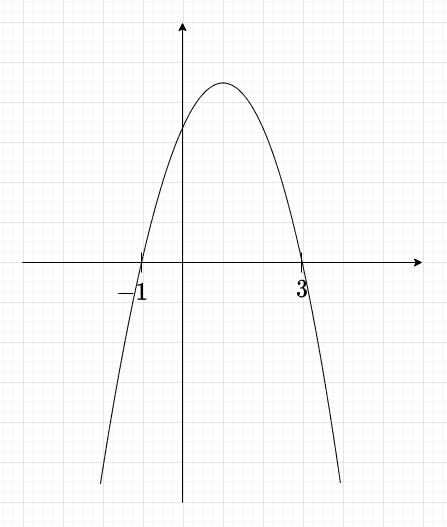
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej , której miejsca zerowe to: i .

A.
B.
C.
D.
Zadanie 3
Funkcja kwadratowa określona wzorem jest malejąca w przedziale
A.
B.
C.
D.
Materiały dodatkowe
Zadanie 1
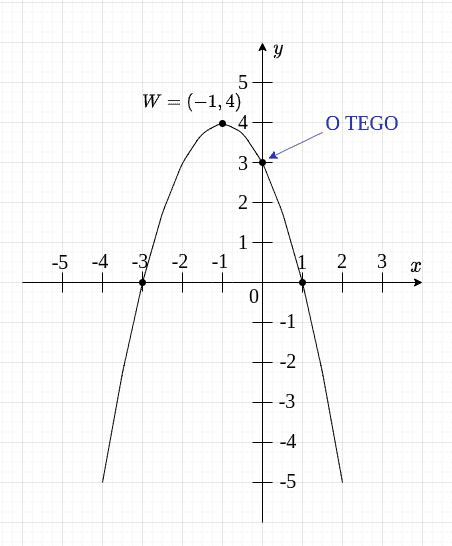
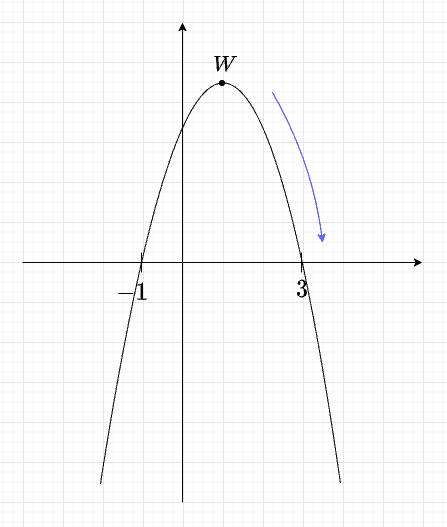
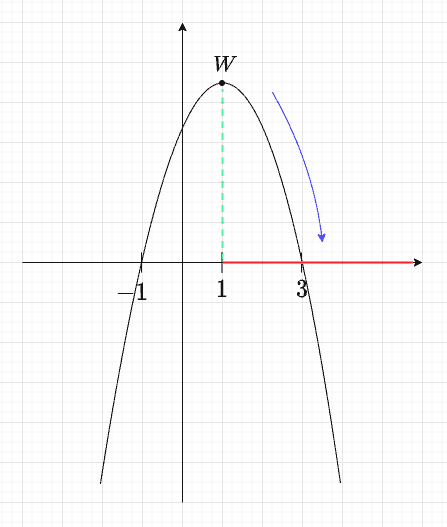
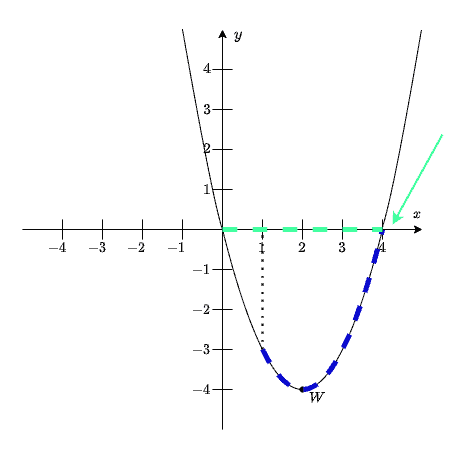
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej . Wierzchołkiem tej paraboli jest punkt . Liczby i to miejsca zerowe funkcji .

A.
B.
C.
D.
Zadanie 2
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej . Wierzchołkiem tej paraboli jest punkt . Liczby i to miejsca zerowe funkcji .

A.
B.
C.
D.
Zadanie 3
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej . Wierzchołkiem tej paraboli jest punkt . Liczby i to miejsca zerowe funkcji .

A.
B.
C.
D.
Materiały dodatkowe
Zadanie 1
Na wykresie funkcji liniowej określonej wzorem leży punkt . Zatem
A.
B.
C.
D.
Zadanie 2
Funkcja kwadratowa określona jest wzorem . Jeżeli , to
A.
B.
C.
D.
Zadanie 3
Liczba jest miejscem zerowym funkcji liniowej , a punkt należy do wykresu tej funkcji. Współczynnik we wzorze tej funkcji jest równy
A.
B.
C.
D.
Zadanie 1
Funkcja określona jest wzorem dla każdej liczby rzeczywistej . Wtedy jest równa
A.
B.
C.
D.